|
1201 |
The centre of those circles which touch the circle x2 + y2 – 8x – 8y = 0, externally and also touch the X- axis, lie on a) A circle b) An ellipse which is not a circle c) A hyperbola d) A parabola
The centre of those circles which touch the circle x2 + y2 – 8x – 8y = 0, externally and also touch the X- axis, lie on a) A circle b) An ellipse which is not a circle c) A hyperbola d) A parabola
|
IIT 2016 |
|
|
1202 |
Solve 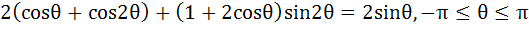
Solve 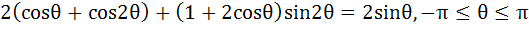
|
IIT 1978 |
|
|
1203 |
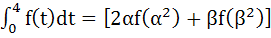 for every 0 < α, β < 2. for every 0 < α, β < 2.
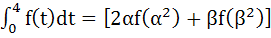 for every 0 < α, β < 2. for every 0 < α, β < 2.
|
IIT 2003 |
|
|
1204 |
Let (x, y) be any point on the parabola y2 = 4x. Let P be the point that divides the line segment from (0, 0) to (x, y) in the ratio of 1 : 3. Then the locus of P is a) x2 = y b) y2 = 2x c) y2 = x d) x2 = 2y
Let (x, y) be any point on the parabola y2 = 4x. Let P be the point that divides the line segment from (0, 0) to (x, y) in the ratio of 1 : 3. Then the locus of P is a) x2 = y b) y2 = 2x c) y2 = x d) x2 = 2y
|
IIT 2011 |
|
|
1205 |
The value of 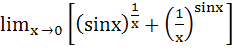 where x > 0 is where x > 0 is a) 0 b) – 1 c) 1 d) 2
The value of 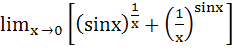 where x > 0 is where x > 0 is a) 0 b) – 1 c) 1 d) 2
|
IIT 2006 |
|
|
1206 |
The value of 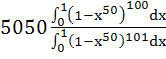 a) 5050 b) 5051 c) 100 d) 101
The value of 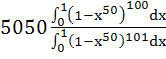 a) 5050 b) 5051 c) 100 d) 101
|
IIT 2006 |
|
|
1207 |
Let the curve C be the mirror image of the parabola y2 = 4x with respect to the line x + y + 4 = 0. If A and B are points of intersection of C with the line y = −5 then the distance between A and B is . . .?
Let the curve C be the mirror image of the parabola y2 = 4x with respect to the line x + y + 4 = 0. If A and B are points of intersection of C with the line y = −5 then the distance between A and B is . . .?
|
IIT 2015 |
|
|
1208 |
Consider the parabola y2 = 8x. Let △1 be the area of the triangle formed by the end points of its latus rectum and the point on the parabola and △2 be the area of the triangle formed by drawing tangent at P and the end points of the latus rectum. Then is
Consider the parabola y2 = 8x. Let △1 be the area of the triangle formed by the end points of its latus rectum and the point on the parabola and △2 be the area of the triangle formed by drawing tangent at P and the end points of the latus rectum. Then is
|
IIT 2011 |
|
|
1209 |
Multiple choices Let g (x) = x f (x), where 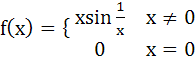 at x = 0 at x = 0 a) g is 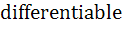 but but 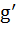 is not continuous is not continuous b) g is 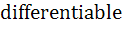 while f is not while f is not c) f and g are both differentiable d) g is 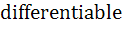 and and 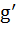 is continuous is continuous
Multiple choices Let g (x) = x f (x), where 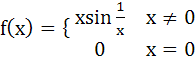 at x = 0 at x = 0 a) g is 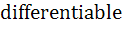 but but 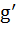 is not continuous is not continuous b) g is 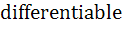 while f is not while f is not c) f and g are both differentiable d) g is 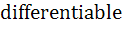 and and 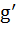 is continuous is continuous
|
IIT 1994 |
|
|
1210 |
A five digit number divisible by 3 is formed using the numerals 0, 1, 2, 3, 4, and 5 without repetition. Total number of ways this can be done is a) At least 30 b) At most 20 c) Exactly 25 d) None of these
A five digit number divisible by 3 is formed using the numerals 0, 1, 2, 3, 4, and 5 without repetition. Total number of ways this can be done is a) At least 30 b) At most 20 c) Exactly 25 d) None of these
|
IIT 1989 |
|
|
1211 |
A rectangle with sides (2m – 1) and (2n – 1) is divided into squares of unit length by drawing parallel lines. Then the number of rectangles possible with odd side lengths is a) mn (m + 1)(n + 1) b) 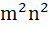 c) 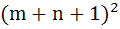 d) 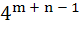
A rectangle with sides (2m – 1) and (2n – 1) is divided into squares of unit length by drawing parallel lines. Then the number of rectangles possible with odd side lengths is a) mn (m + 1)(n + 1) b) 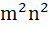 c) 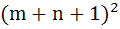 d) 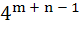
|
IIT 2005 |
|
|
1212 |
Let g (x) be a polynomial of degree one and f (x) be defined by 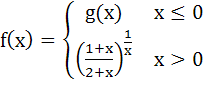 Find the continuous function f (x) satisfying 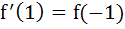 a) 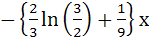 b) 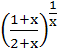 c) 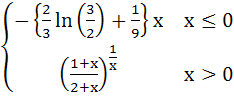 d) None of the above
Let g (x) be a polynomial of degree one and f (x) be defined by 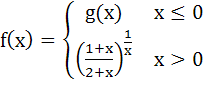 Find the continuous function f (x) satisfying 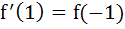 a) 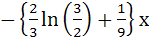 b) 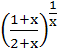 c) 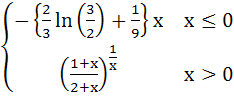 d) None of the above
|
IIT 1987 |
|
|
1213 |
In how many ways can a pack of 52 cards be divided equally amongst 4 players in order?
In how many ways can a pack of 52 cards be divided equally amongst 4 players in order?
|
IIT 1979 |
|
|
1214 |
Find the interval in which ‘a’ lies for which the line y + x = 0 bisects the chord drawn from the point 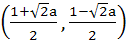 to the circle to the circle 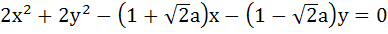
Find the interval in which ‘a’ lies for which the line y + x = 0 bisects the chord drawn from the point 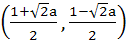 to the circle to the circle 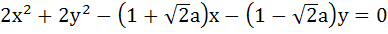
|
IIT 1996 |
|
|
1215 |
The points on the curve 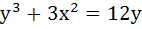 where the tangent is vertical, is (are) where the tangent is vertical, is (are) a) 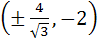 b) 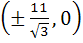 c) 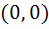 d) 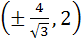
The points on the curve 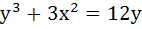 where the tangent is vertical, is (are) where the tangent is vertical, is (are) a) 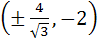 b) 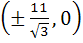 c) 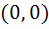 d) 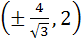
|
IIT 2002 |
|
|
1216 |
Let T1, T2 be two tangents drawn from (−2, 0) onto the circle C: x2 + y2 = 1. Determine the circle touching C and having T1, T2 as their pair of tangents. Further find the equation of all possible common tangents to the circles, when taken two at a time.
Let T1, T2 be two tangents drawn from (−2, 0) onto the circle C: x2 + y2 = 1. Determine the circle touching C and having T1, T2 as their pair of tangents. Further find the equation of all possible common tangents to the circles, when taken two at a time.
|
IIT 1999 |
|
|
1217 |
Let 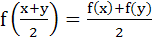 for all real x and y. If for all real x and y. If 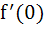 exists and exists and 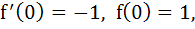 then find f(2) then find f(2) a) – 1 b) 0 c) 1 d) 2
Let 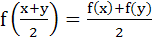 for all real x and y. If for all real x and y. If 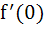 exists and exists and 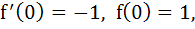 then find f(2) then find f(2) a) – 1 b) 0 c) 1 d) 2
|
IIT 1995 |
|
|
1218 |
Let 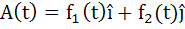 and and 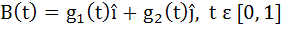 where where 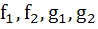 are continuous functions. If A(t) and B(t) are non-zero vectors for all t and are continuous functions. If A(t) and B(t) are non-zero vectors for all t and A(0) = 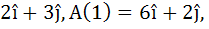 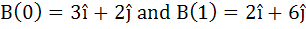
then A(t) and b(t) are parallel for some t. a) True b) False
Let 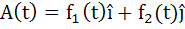 and and 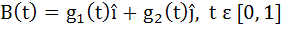 where where 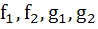 are continuous functions. If A(t) and B(t) are non-zero vectors for all t and are continuous functions. If A(t) and B(t) are non-zero vectors for all t and A(0) = 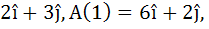 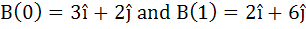
then A(t) and b(t) are parallel for some t. a) True b) False
|
IIT 2001 |
|
|
1219 |
Let n be any positive integer. Prove that 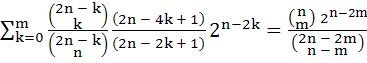
For each non negative integer m ≤ n
Let n be any positive integer. Prove that 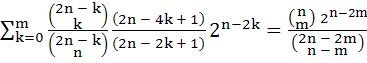
For each non negative integer m ≤ n
|
IIT 1999 |
|
|
1220 |
Find the centre and radius of the circle formed by all the points represented by 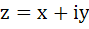 satisfying the relation satisfying the relation 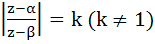 where α and β are complex numbers given by where α and β are complex numbers given by
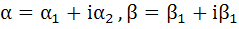
|
IIT 2004 |
|
|
1221 |
Using permutation or otherwise prove that 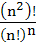 is an integer, where n is a positive integer. is an integer, where n is a positive integer.
Using permutation or otherwise prove that 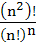 is an integer, where n is a positive integer. is an integer, where n is a positive integer.
|
IIT 2004 |
|
|
1222 |
Three circles of radii 3, 4 and 5 units touch each other externally and tangents drawn at the points of contact intersect at P. Find the distance between P and the point of contact.
Three circles of radii 3, 4 and 5 units touch each other externally and tangents drawn at the points of contact intersect at P. Find the distance between P and the point of contact.
|
IIT 2005 |
|
|
1223 |
In ΔABC, D is the midpoint of BC. If AD is perpendicular to AC then 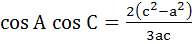 . . a) True b) False
In ΔABC, D is the midpoint of BC. If AD is perpendicular to AC then 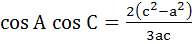 . . a) True b) False
|
IIT 1980 |
|
|
1224 |
A function f : R  R where R is the set of real numbers is defined by f (x) = R where R is the set of real numbers is defined by f (x) = 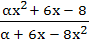 . Find the interval of values of α for which f is onto. Is the function one to one for α = 3? Justify your answer. . Find the interval of values of α for which f is onto. Is the function one to one for α = 3? Justify your answer. a) 2 ≤ α ≤ 14 b) α ≥ 2 c) α ≤ 14 d) none of the above
A function f : R  R where R is the set of real numbers is defined by f (x) = R where R is the set of real numbers is defined by f (x) = 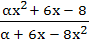 . Find the interval of values of α for which f is onto. Is the function one to one for α = 3? Justify your answer. . Find the interval of values of α for which f is onto. Is the function one to one for α = 3? Justify your answer. a) 2 ≤ α ≤ 14 b) α ≥ 2 c) α ≤ 14 d) none of the above
|
IIT 1996 |
|
|
1225 |
If f1 ( x ) and f2 ( x ) are defined by domains D1 and D2 respectively, then f1 ( x ) + f2 ( x ) is defined as on D1 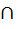 D2. D2. a) True b) False
If f1 ( x ) and f2 ( x ) are defined by domains D1 and D2 respectively, then f1 ( x ) + f2 ( x ) is defined as on D1 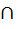 D2. D2. a) True b) False
|
IIT 1988 |
|