|
151 |
Suppose that the normals drawn at three different points on the parabola 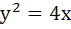 pass through the point (h, 0). Show that h > 2. pass through the point (h, 0). Show that h > 2.
Suppose that the normals drawn at three different points on the parabola 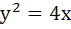 pass through the point (h, 0). Show that h > 2. pass through the point (h, 0). Show that h > 2.
|
IIT 1981 |
03:52 min
|
|
152 |
Through the vertex O of the parabola 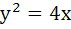 chords OP and OQ are drawn at right angles. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the midpoint of PQ. chords OP and OQ are drawn at right angles. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the midpoint of PQ.
Through the vertex O of the parabola 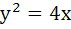 chords OP and OQ are drawn at right angles. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the midpoint of PQ. chords OP and OQ are drawn at right angles. Show that for all positions of P, PQ cuts the axis of the parabola at a fixed point. Also find the locus of the midpoint of PQ.
|
IIT 1994 |
05:22 min
|
|
153 |
For all x ε ( 0, 1 ) a) 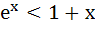 b) ln (1 + x) < x c) sinx > x d) lnx > x
For all x ε ( 0, 1 ) a) 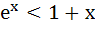 b) ln (1 + x) < x c) sinx > x d) lnx > x
|
IIT 2000 |
02:40 min
|
|
154 |
Given x = cy + bz, y = az + cx, z = bx + ay where x, y, z are not all zero, prove that a2 + b2 + c2 + 2abc = 1
Given x = cy + bz, y = az + cx, z = bx + ay where x, y, z are not all zero, prove that a2 + b2 + c2 + 2abc = 1
|
IIT 1978 |
03:30 min
|
|
155 |
Let 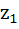 and and 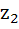 are two complex numbers such that are two complex numbers such that 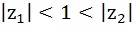 then prove that then prove that 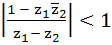 . .
|
IIT 2003 |
04:08 min
|
|
156 |
The number of values of k for which the system of equations (k + 1) x + 8y = 4k kx + ( k + 3 ) y = 3k – 1 has infinitely many solutions is a) 0 b) 1 c) 2 d) Infinity
The number of values of k for which the system of equations (k + 1) x + 8y = 4k kx + ( k + 3 ) y = 3k – 1 has infinitely many solutions is a) 0 b) 1 c) 2 d) Infinity
|
IIT 2002 |
02:56 min
|
|
157 |
Without expanding a determinant at any stage show that
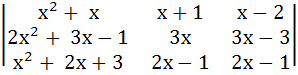 = Ax + B = Ax + B where A, B are non-zero constants
Without expanding a determinant at any stage show that
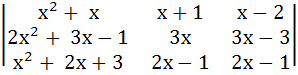 = Ax + B = Ax + B where A, B are non-zero constants
|
IIT 1982 |
04:06 min
|
|
158 |
True/False
If the complex numbers 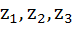 represent the vertices of an equilateral triangle with represent the vertices of an equilateral triangle with 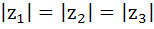 then then 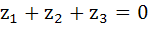 . . a) True b) False
True/False
If the complex numbers 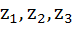 represent the vertices of an equilateral triangle with represent the vertices of an equilateral triangle with 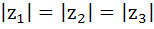 then then 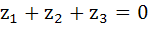 . . a) True b) False
|
IIT 1984 |
02:27 min
|
|
159 |
The order of the differential equation whose general solution is given by 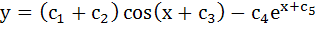 is is a) 5 b) 4 c) 3 d) 2
The order of the differential equation whose general solution is given by 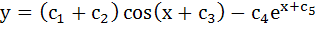 is is a) 5 b) 4 c) 3 d) 2
|
IIT 1998 |
03:42 min
|
|
160 |
If f (x) =  a) f (x) is a strictly increasing function b) f (x) has a local maxima c) f (x) is a strictly decreasing function d) f (x) is bounded
If f (x) =  a) f (x) is a strictly increasing function b) f (x) has a local maxima c) f (x) is a strictly decreasing function d) f (x) is bounded
|
IIT 2004 |
02:07 min
|
|
161 |
Let Δa = 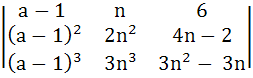
Then show that 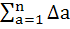 = c, a constant. = c, a constant.
Let Δa = 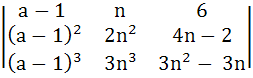
Then show that 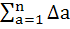 = c, a constant. = c, a constant.
|
IIT 1989 |
05:34 min
|
|
162 |
For any two complex numbers 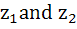 and any real numbers and any real numbers 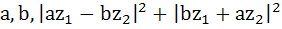 is equal to . . . . is equal to . . . . a) 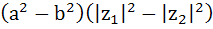 b) 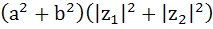 c) 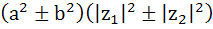 d) 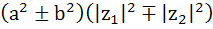
For any two complex numbers 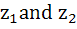 and any real numbers and any real numbers 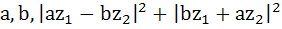 is equal to . . . . is equal to . . . . a) 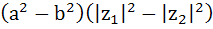 b) 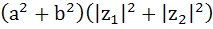 c) 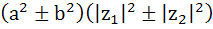 d) 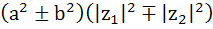
|
IIT 1988 |
02:43 min
|
|
163 |
The locus of a variable point whose distance from 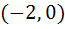 is is  times its distance from the line times its distance from the line 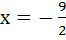 is is a) Ellipse b) Parabola c) Hyperbola d) None of these
The locus of a variable point whose distance from 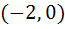 is is  times its distance from the line times its distance from the line 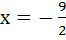 is is a) Ellipse b) Parabola c) Hyperbola d) None of these
|
IIT 1994 |
02:40 min
|
|
164 |
If 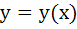 and and 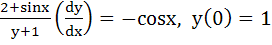 then then 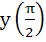 equals equals a)  b)  c) 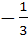 d) 1
If 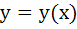 and and 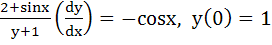 then then 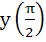 equals equals a)  b)  c) 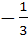 d) 1
|
IIT 2004 |
03:00 min
|
|
165 |
The second degree polynomial satisfying f (0) = 0, f (1) = 1, 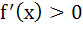 for all x ε [0, 1] is for all x ε [0, 1] is a) 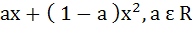 b) No such polynomial c) 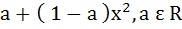 d) 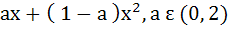
The second degree polynomial satisfying f (0) = 0, f (1) = 1, 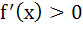 for all x ε [0, 1] is for all x ε [0, 1] is a) 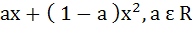 b) No such polynomial c) 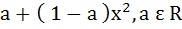 d) 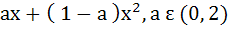
|
IIT 2005 |
03:08 min
|
|
166 |
For a > 0, d > 0, find the value of the determinant
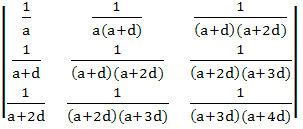 a) 0 b) 1 c) 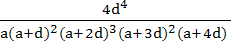 d) 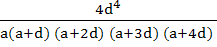
For a > 0, d > 0, find the value of the determinant
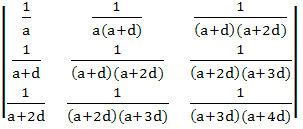 a) 0 b) 1 c) 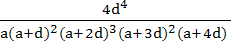 d) 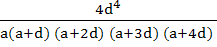
|
IIT 1996 |
05:35 min
|
|
167 |
Multiple choices For real x, the function 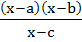 will assume all real values provided will assume all real values provided a) 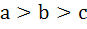 b) 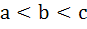 c) 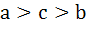 d) 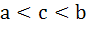
Multiple choices For real x, the function 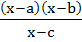 will assume all real values provided will assume all real values provided a) 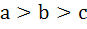 b) 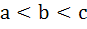 c) 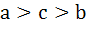 d) 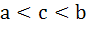
|
IIT 1984 |
05:06 min
|
|
168 |
If the matrix A is equal to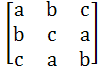 where a, b, c are real positive numbers, abc = 1 and ATA = I then find the value of a3 + b3 + c3. where a, b, c are real positive numbers, abc = 1 and ATA = I then find the value of a3 + b3 + c3. a) 1 b) 2 c) 3 d) 4
If the matrix A is equal to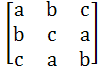 where a, b, c are real positive numbers, abc = 1 and ATA = I then find the value of a3 + b3 + c3. where a, b, c are real positive numbers, abc = 1 and ATA = I then find the value of a3 + b3 + c3. a) 1 b) 2 c) 3 d) 4
|
IIT 2003 |
04:04 min
|
|
169 |
Prove if α, β are roots of the equation 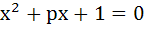 and γ, δ are roots of and γ, δ are roots of 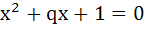 then show that then show that
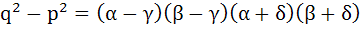
|
IIT 1978 |
03:39 min
|
|
170 |
If the function f: [0, 4] → ℝ is differentiable, then for a, b ε [0, 4] 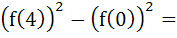 a) 8 f (a) f (b) b) 8 f (a) f '(b) c) 8 f '(a) f (b) d) 8 f '(a) f '(b)
If the function f: [0, 4] → ℝ is differentiable, then for a, b ε [0, 4] 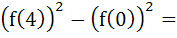 a) 8 f (a) f (b) b) 8 f (a) f '(b) c) 8 f '(a) f (b) d) 8 f '(a) f '(b)
|
IIT 2003 |
01:57 min
|
|
171 |
Find the equation of the common tangent in the first quadrant to the circle 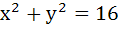 and the ellipse and the ellipse 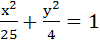 . Also find the length of the intercept of the tangent between the coordinate axis. . Also find the length of the intercept of the tangent between the coordinate axis.
Find the equation of the common tangent in the first quadrant to the circle 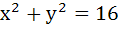 and the ellipse and the ellipse 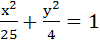 . Also find the length of the intercept of the tangent between the coordinate axis. . Also find the length of the intercept of the tangent between the coordinate axis.
|
IIT 2005 |
06:45 min
|
|
172 |
The value of the determinant 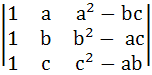 is ………… is ………… a) 0 b) 1 c) a2 + b2 + c2 – abc d) a2 + b2 + c2 – 3abc
The value of the determinant 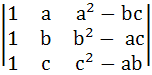 is ………… is ………… a) 0 b) 1 c) a2 + b2 + c2 – abc d) a2 + b2 + c2 – 3abc
|
IIT 1988 |
02:49 min
|
|
173 |
The equation 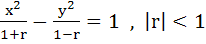 represents represents a) An ellipse b) A hyperbola c) A circle d) None of these
The equation 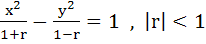 represents represents a) An ellipse b) A hyperbola c) A circle d) None of these
|
IIT 1981 |
01:03 min
|
|
174 |
Find all the real values of x which satisfy 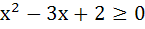 and and 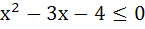 . .
Find all the real values of x which satisfy 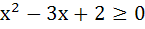 and and 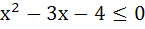 . .
|
IIT 1983 |
02:29 min
|
|
175 |
For the hyperbola 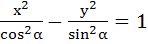 which of the following remains constant with change in α which of the following remains constant with change in α a) Abscissae of vertices b) Abscissae of focii c) Eccentricity d) Directrix
For the hyperbola 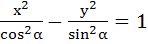 which of the following remains constant with change in α which of the following remains constant with change in α a) Abscissae of vertices b) Abscissae of focii c) Eccentricity d) Directrix
|
IIT 2003 |
01:32 min
|