|
1301 |
Find the area bounded by the curve x2 = 4y and the straight line
x = 4y – 2. a) 3/2 b) 3/4 c) 9/4 d) 9/8
Find the area bounded by the curve x2 = 4y and the straight line
x = 4y – 2. a) 3/2 b) 3/4 c) 9/4 d) 9/8
|
IIT 1981 |
|
|
1302 |
If f(x) and g(x) are differentiable functions for 0 ≤ x ≤ 1 such that f(0) = 2, g(0) = 0, f(1) = 6, g(1) = 2 then show that there exists c satisfying 0 < c < 1 and 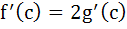 . . a) 0 < c < 1 and 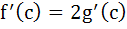 b) 0 < c < 1 and 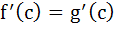 c) 0 < c < 1 and 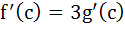 d) 0 < c < 1 and 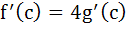
If f(x) and g(x) are differentiable functions for 0 ≤ x ≤ 1 such that f(0) = 2, g(0) = 0, f(1) = 6, g(1) = 2 then show that there exists c satisfying 0 < c < 1 and 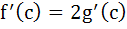 . . a) 0 < c < 1 and 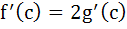 b) 0 < c < 1 and 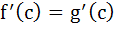 c) 0 < c < 1 and 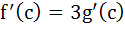 d) 0 < c < 1 and 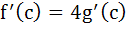
|
IIT 1982 |
|
|
1303 |
Let a > 0, b > 0, c > 0 then both the roots of the equation 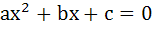 a) are real and positive b) have negative real parts c) have positive real parts d) none of these
Let a > 0, b > 0, c > 0 then both the roots of the equation 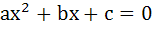 a) are real and positive b) have negative real parts c) have positive real parts d) none of these
|
IIT 1979 |
|
|
1304 |
If f(x) is a continuous function defined for 1 ≤ x ≤ 3. If f(x) takes rational values for all x and f(2) = 10 then f(1.5) = . . . . a) 2 b) 5 c) 10 d) 20
If f(x) is a continuous function defined for 1 ≤ x ≤ 3. If f(x) takes rational values for all x and f(2) = 10 then f(1.5) = . . . . a) 2 b) 5 c) 10 d) 20
|
IIT 1997 |
|
|
1305 |
If x, y, z are real and distinct then 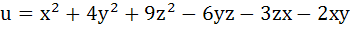 is always is always a) Non – negative b) Non – positive c) Zero d) None of these
If x, y, z are real and distinct then 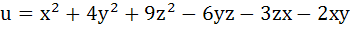 is always is always a) Non – negative b) Non – positive c) Zero d) None of these
|
IIT 2005 |
|
|
1306 |
Match the following
Let [x] denote the greatest integer less than or equal to x | Column 1 | Column 2 | | i) x|x| | A)continuous in 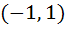 | | ii) 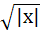 | B)Differentiable in 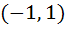 | | iii) x + [x] | C)Steadily increasing in 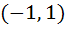 | | iv) |x – 1| + |x + 1| | D) Not differentiable at least at one point in 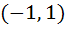 | a) (i)→ A, B, C, (ii)→ A, D, (iii)→ C, D, (iv)→ A, B b) (i)→ A, (ii)→ A, (iii)→ C, (iv)→ B c) (i)→ B, (ii)→ D, (iii)→ C, (iv)→ A d) (i)→ A, B, (ii)→ A, D, (iii)→ C, D, (iv)→ B
Match the following
Let [x] denote the greatest integer less than or equal to x | Column 1 | Column 2 | | i) x|x| | A)continuous in 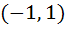 | | ii) 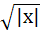 | B)Differentiable in 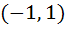 | | iii) x + [x] | C)Steadily increasing in 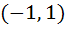 | | iv) |x – 1| + |x + 1| | D) Not differentiable at least at one point in 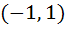 | a) (i)→ A, B, C, (ii)→ A, D, (iii)→ C, D, (iv)→ A, B b) (i)→ A, (ii)→ A, (iii)→ C, (iv)→ B c) (i)→ B, (ii)→ D, (iii)→ C, (iv)→ A d) (i)→ A, B, (ii)→ A, D, (iii)→ C, D, (iv)→ B
|
IIT 2007 |
|
|
1307 |
(One or more than one correct answer)
If 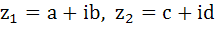 are complex numbers such that are complex numbers such that 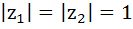 and and 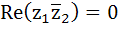 then the pair of complex numbers then the pair of complex numbers 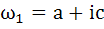 and and 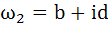 satisfy satisfy a) 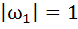 b) 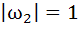 c) 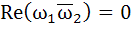 d) None of these
|
IIT 1985 |
|
|
1308 |
Let ABCD be a square with side of length 2 units. C2 is the circle through the vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. A line M is drawn through A parallel to BD. Point S moves such that the distance from the line BD and the vertex A are equal. If the locus of S cuts M at T2 and T3 and AC at T1, then find the area of △T1T2T3.
Let ABCD be a square with side of length 2 units. C2 is the circle through the vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. A line M is drawn through A parallel to BD. Point S moves such that the distance from the line BD and the vertex A are equal. If the locus of S cuts M at T2 and T3 and AC at T1, then find the area of △T1T2T3.
|
IIT 2006 |
|
|
1309 |
Express 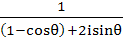 in the form A + iB in the form A + iB a) 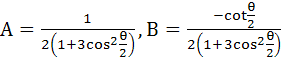 b) 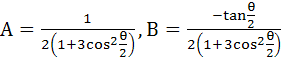 c) 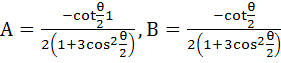 d) 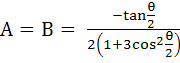
Express 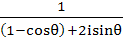 in the form A + iB in the form A + iB a) 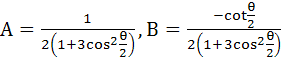 b) 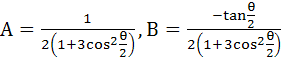 c) 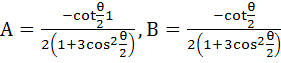 d) 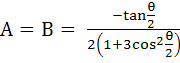
|
IIT 1979 |
|
|
1310 |
Find the area bounded by the curves
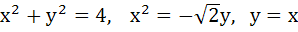 a) 1/6 b) 1/3 c) π d) 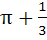
Find the area bounded by the curves
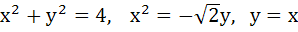 a) 1/6 b) 1/3 c) π d) 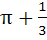
|
IIT 1986 |
|
|
1311 |
If the line x – 1 = 0 is the directrix of the parabola y2 – kx + 8 = 0, then one of the values of k is a)  b) 8 c) 4 d) 
If the line x – 1 = 0 is the directrix of the parabola y2 – kx + 8 = 0, then one of the values of k is a)  b) 8 c) 4 d) 
|
IIT 2000 |
|
|
1312 |
Find the area bounded by the curves x2 + y2 = 25, 4y = |4 – x2| and x = 0 above the X–axis. a) 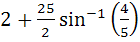 b) 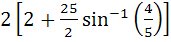 c) 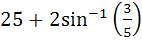 d) 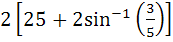
Find the area bounded by the curves x2 + y2 = 25, 4y = |4 – x2| and x = 0 above the X–axis. a) 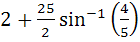 b) 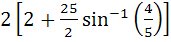 c) 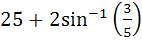 d) 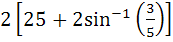
|
IIT 1987 |
|
|
1313 |
If sinA sinB sinC + cosA cosB = 1then the value of sinC is
If sinA sinB sinC + cosA cosB = 1then the value of sinC is
|
IIT 2006 |
|
|
1314 |
Let 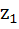 = 10 + 6i and = 10 + 6i and 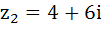 . If z is a complex number such that argument of . If z is a complex number such that argument of 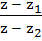 is is 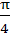 then prove that then prove that 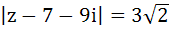 . .
|
IIT 1990 |
|
|
1315 |
Compute the area of the region bounded by the curves
y = exlnx and 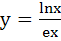 a) 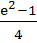 b) 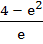 c) 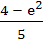 d) 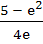
Compute the area of the region bounded by the curves
y = exlnx and 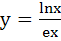 a) 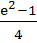 b) 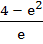 c) 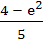 d) 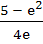
|
IIT 1990 |
|
|
1316 |
A plane passes through (1, −2, 1) and is perpendicular to the two planes 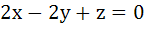 and and 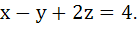 The distance of the plane from the point (1, 2, 2) is. The distance of the plane from the point (1, 2, 2) is.
A plane passes through (1, −2, 1) and is perpendicular to the two planes 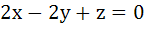 and and 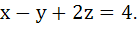 The distance of the plane from the point (1, 2, 2) is. The distance of the plane from the point (1, 2, 2) is.
|
IIT 2006 |
|
|
1317 |
What normal to the curve y = x2 forms the shortest normal? a) 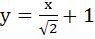 b) 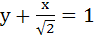 c) 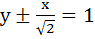 d) y = x + 1
What normal to the curve y = x2 forms the shortest normal? a) 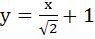 b) 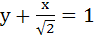 c) 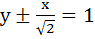 d) y = x + 1
|
IIT 1992 |
|
|
1318 |
(Multiple choices)
The value of θ lying between θ = 0 and θ =  and satisfying the equation and satisfying the equation
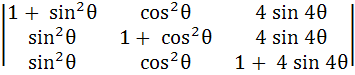 = 0 are = 0 are a) 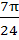 b) 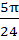 c) 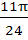 d) 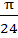
(Multiple choices)
The value of θ lying between θ = 0 and θ =  and satisfying the equation and satisfying the equation
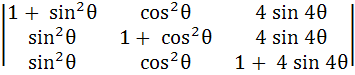 = 0 are = 0 are a) 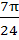 b) 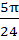 c) 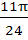 d) 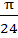
|
IIT 1988 |
|
|
1319 |
Let a complex number α, α ≠ 1, be root of the equation 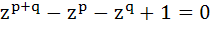 where p and q are distinct primes. Show that either where p and q are distinct primes. Show that either 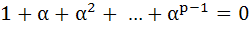 or or 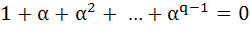 , but not together. , but not together.
|
IIT 2002 |
|
|
1320 |
The circle x2 + y2 = 1 cuts the X–axis at P and Q. Another circle with centre at Q and variable radius intersects the first circle at R above the X–axis and the line segment PQ at S. Find the maximum area of ΔQRS. a) 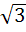 b) 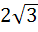 c) 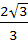 d) 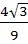
The circle x2 + y2 = 1 cuts the X–axis at P and Q. Another circle with centre at Q and variable radius intersects the first circle at R above the X–axis and the line segment PQ at S. Find the maximum area of ΔQRS. a) 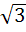 b) 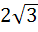 c) 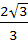 d) 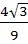
|
IIT 1994 |
|
|
1321 |
From a point A common tangents are drawn to the circle 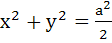 and the parabola and the parabola 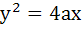 . Find the area of the quadrilateral formed by the common tangents drawn from A and the chords of contact of the circle and the parabola. . Find the area of the quadrilateral formed by the common tangents drawn from A and the chords of contact of the circle and the parabola.
From a point A common tangents are drawn to the circle 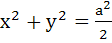 and the parabola and the parabola 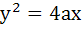 . Find the area of the quadrilateral formed by the common tangents drawn from A and the chords of contact of the circle and the parabola. . Find the area of the quadrilateral formed by the common tangents drawn from A and the chords of contact of the circle and the parabola.
|
IIT 1996 |
|
|
1322 |
True/False
For the complex numbers 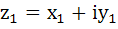 and and 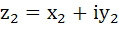 we write we write 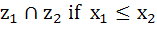 and and 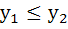 then for all complex numbers z with then for all complex numbers z with 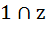 we have we have 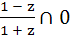 . . a) True b) False
|
IIT 1981 |
|
|
1323 |
Let 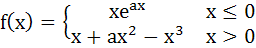
where a is a positive constant. Find the interval in which 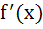 is increasing. is increasing. a) 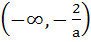 b) 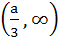 c) 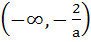 d) 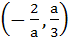
Let 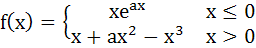
where a is a positive constant. Find the interval in which 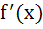 is increasing. is increasing. a) 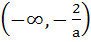 b) 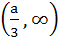 c) 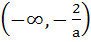 d) 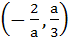
|
IIT 1996 |
|
|
1324 |
Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a, b, c and d denote the lengths of the sides of the quadrilateral; prove that
2 ≤ a2 + b2 + c2 + d2 ≤ 4
Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a, b, c and d denote the lengths of the sides of the quadrilateral; prove that
2 ≤ a2 + b2 + c2 + d2 ≤ 4
|
IIT 1997 |
|
|
1325 |
The number of ordered pairs satisfying the equations
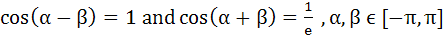 is is a) 4 b) 2 c) 0 d) 1
The number of ordered pairs satisfying the equations
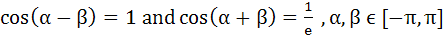 is is a) 4 b) 2 c) 0 d) 1
|
IIT 2005 |
|