|
1276 |
Let –1 ≤ p ≤ 1. Show that the equation 4x3 – 3x – p = 0 has a unique root in the interval 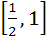 and identify it. and identify it. a) p b) p/3 c) 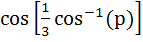 d) 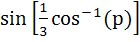
Let –1 ≤ p ≤ 1. Show that the equation 4x3 – 3x – p = 0 has a unique root in the interval 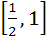 and identify it. and identify it. a) p b) p/3 c) 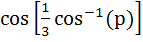 d) 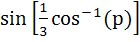
|
IIT 2001 |
|
|
1277 |
Find the coordinates of all points P on the ellipse 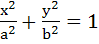 , for which the area of △PON is maximum where O denotes the origin and N the feet of perpendicular from O to the tangent at P. , for which the area of △PON is maximum where O denotes the origin and N the feet of perpendicular from O to the tangent at P.
Find the coordinates of all points P on the ellipse 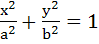 , for which the area of △PON is maximum where O denotes the origin and N the feet of perpendicular from O to the tangent at P. , for which the area of △PON is maximum where O denotes the origin and N the feet of perpendicular from O to the tangent at P.
|
IIT 1999 |
|
|
1278 |
Determine the equation of the curve passing through origin in the form 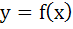 which satisfies the differential equation which satisfies the differential equation 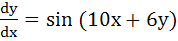
Determine the equation of the curve passing through origin in the form 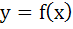 which satisfies the differential equation which satisfies the differential equation 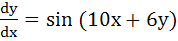
|
IIT 1996 |
|
|
1279 |
If α, β are roots of 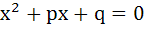 and γ, δ are roots of and γ, δ are roots of 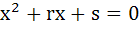 then evaluate then evaluate 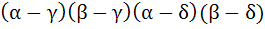 in terms of p, q, r, s. in terms of p, q, r, s.
|
IIT 1979 |
|
|
1280 |
If p(x) = 51x101 – 2323x100 – 45x + 1035, using Rolle’s theorem prove that at least one root lies between 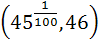 . .
If p(x) = 51x101 – 2323x100 – 45x + 1035, using Rolle’s theorem prove that at least one root lies between 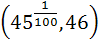 . .
|
IIT 2004 |
|
|
1281 |
For what values of m does the system of equations 3x + my = m, 2x – 5y = 20 have solutions satisfying x > 0, y > 0? a) m ε (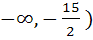 b) m ε (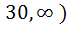 c) m ε (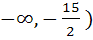 ∪ ( ∪ (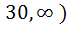 d) m ε (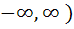
For what values of m does the system of equations 3x + my = m, 2x – 5y = 20 have solutions satisfying x > 0, y > 0? a) m ε (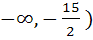 b) m ε (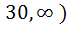 c) m ε (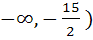 ∪ ( ∪ (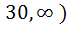 d) m ε (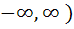
|
IIT 1980 |
|
|
1282 |
Given 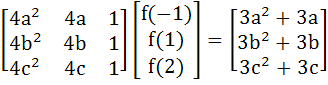
and f(x) is a quadratic polynomial. V is a point of maximum of f(x) and ‘A’ is the point where f(x) cuts the X–axis. ‘B’ is a point such that AB subtends a right angle at V. Find the area between chord AB and f(x).
a) 125 b) 125/2 c) 125/3 d) 125/6
Given 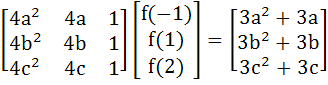
and f(x) is a quadratic polynomial. V is a point of maximum of f(x) and ‘A’ is the point where f(x) cuts the X–axis. ‘B’ is a point such that AB subtends a right angle at V. Find the area between chord AB and f(x).
a) 125 b) 125/2 c) 125/3 d) 125/6
|
IIT 2005 |
|
|
1283 |
The area enclosed within the curve |x| + |y| = 1 is . . . a) 1 b) 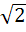 c) 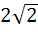 d) 2
The area enclosed within the curve |x| + |y| = 1 is . . . a) 1 b) 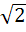 c) 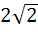 d) 2
|
IIT 1981 |
|
|
1284 |
Let a hyperbola pass through the foci of the ellipse 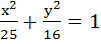 . The transverse and conjugate axes of the hyperbola coincide with the major and minor axes of the given ellipse. Also the product of the eccentricity of the given ellipse and hyperbola is 1 then . The transverse and conjugate axes of the hyperbola coincide with the major and minor axes of the given ellipse. Also the product of the eccentricity of the given ellipse and hyperbola is 1 then a) Equation of the hyperbola is 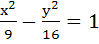 b) Equation of the hyperbola is 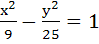 c) Focus of the hyperbola is (5, 0) d) Vertex of the hyperbola is 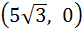
Let a hyperbola pass through the foci of the ellipse 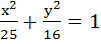 . The transverse and conjugate axes of the hyperbola coincide with the major and minor axes of the given ellipse. Also the product of the eccentricity of the given ellipse and hyperbola is 1 then . The transverse and conjugate axes of the hyperbola coincide with the major and minor axes of the given ellipse. Also the product of the eccentricity of the given ellipse and hyperbola is 1 then a) Equation of the hyperbola is 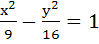 b) Equation of the hyperbola is 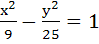 c) Focus of the hyperbola is (5, 0) d) Vertex of the hyperbola is 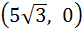
|
IIT 2006 |
|
|
1285 |
The integral is equal to a) 2 b) 4 c) 1 d) 6
The integral is equal to a) 2 b) 4 c) 1 d) 6
|
IIT 2015 |
|
|
1286 |
Fifteen coupons are numbered 1, 2, 3, . . . ., 15 respectively. Seven coupons are selected at random one at a time with replacement. The probability that the largest number appearing on a selected coupon is 9 is a) 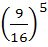 b) 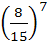 c) 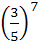 d) None of these
Fifteen coupons are numbered 1, 2, 3, . . . ., 15 respectively. Seven coupons are selected at random one at a time with replacement. The probability that the largest number appearing on a selected coupon is 9 is a) 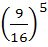 b) 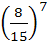 c) 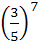 d) None of these
|
IIT 1983 |
|
|
1287 |
Match the statement of column 1 and the properties of column 2 | Column 1 | Column 2 | | i) Two intersecting circles | A. Have a common tangent | | ii) Two mutually external circles | B. Have a common normal | | iii) Two circles one strictly inside the other | C. Do not have a common tangent | | iv) Two branches of a hyperbola | D. Do not have a common normal |
Match the statement of column 1 and the properties of column 2 | Column 1 | Column 2 | | i) Two intersecting circles | A. Have a common tangent | | ii) Two mutually external circles | B. Have a common normal | | iii) Two circles one strictly inside the other | C. Do not have a common tangent | | iv) Two branches of a hyperbola | D. Do not have a common normal |
|
IIT 2007 |
|
|
1288 |
The value of the integral is equal to a) b) c) d)
The value of the integral is equal to a) b) c) d)
|
IIT 2011 |
|
|
1289 |
Let g(x) be a function of x defined on (−1, 1). If the area of the equilateral triangle with two of its vertices as (0, 0) and [x, g(x)] is 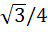 , then the function g(x) is , then the function g(x) is a) 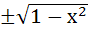 b) 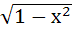 c) 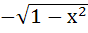 d) None of the above
Let g(x) be a function of x defined on (−1, 1). If the area of the equilateral triangle with two of its vertices as (0, 0) and [x, g(x)] is 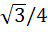 , then the function g(x) is , then the function g(x) is a) 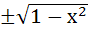 b) 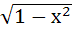 c) 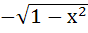 d) None of the above
|
IIT 1989 |
|
|
1290 |
Show that the integral of 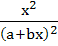 is is 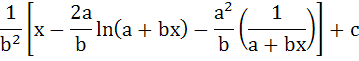
Show that the integral of 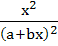 is is 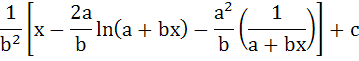
|
IIT 1979 |
|
|
1291 |
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The point of contacts of C with its sides PQ, QR and RP are D, E, F respectively. The line PQ is given by 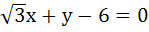 and the point D is and the point D is 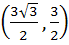 . Further, it is given that the origin and the centre of C are on the same side of the line PQ. The equation of circle C is . Further, it is given that the origin and the centre of C are on the same side of the line PQ. The equation of circle C is a) 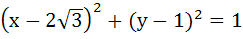 b) 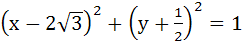 c) 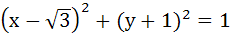 d) 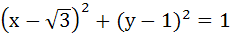
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The point of contacts of C with its sides PQ, QR and RP are D, E, F respectively. The line PQ is given by 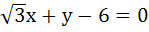 and the point D is and the point D is 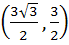 . Further, it is given that the origin and the centre of C are on the same side of the line PQ. The equation of circle C is . Further, it is given that the origin and the centre of C are on the same side of the line PQ. The equation of circle C is a) 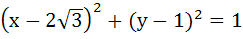 b) 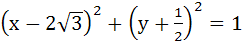 c) 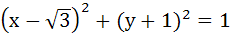 d) 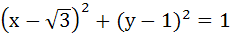
|
IIT 2008 |
|
|
1292 |
One or more than one correct options Let F : ℝ → (0, 1) be a continuous function. Then which of the following function(s) has (have) the value zero at some point in the interval (0, 1)? a) b) c) d)
One or more than one correct options Let F : ℝ → (0, 1) be a continuous function. Then which of the following function(s) has (have) the value zero at some point in the interval (0, 1)? a) b) c) d)
|
IIT 2017 |
|
|
1293 |
Consider a branch of the hyperbola
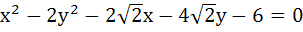
with vertex at the point A. Let B be one of the end points of its latus rectum. If C is the focus of the hyperbola nearest to the point A, then the area of triangle ABC is a) 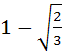 b) 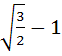 c) 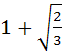 d) 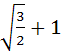
Consider a branch of the hyperbola
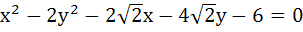
with vertex at the point A. Let B be one of the end points of its latus rectum. If C is the focus of the hyperbola nearest to the point A, then the area of triangle ABC is a) 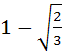 b) 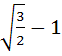 c) 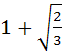 d) 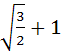
|
IIT 2008 |
|
|
1294 |
One or more than one correct options The value(s) of is (are) a) b) c) d)
One or more than one correct options The value(s) of is (are) a) b) c) d)
|
IIT 2010 |
|
|
1295 |
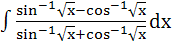 = = 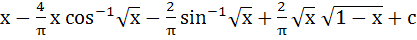
a) True b) False
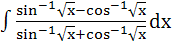 = = 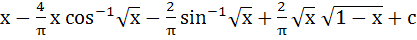
a) True b) False
|
IIT 1986 |
|
|
1296 |
For non-zero vectors a, b, c, 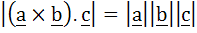 holds if and only if holds if and only if a) a . b = 0, b . c = 0 b) b . c = 0, c . a = 0 c) c . a = 0, a . b = 0 d) a . b = 0, b . c = 0, c . a = 0
For non-zero vectors a, b, c, 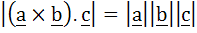 holds if and only if holds if and only if a) a . b = 0, b . c = 0 b) b . c = 0, c . a = 0 c) c . a = 0, a . b = 0 d) a . b = 0, b . c = 0, c . a = 0
|
IIT 1982 |
|
|
1297 |
equals a) 8 b) 2 c) 4 d) 0
equals a) 8 b) 2 c) 4 d) 0
|
IIT 2014 |
|
|
1298 |
The value of is a) 4 b) 0 c) 2 d) 6
The value of is a) 4 b) 0 c) 2 d) 6
|
IIT 2014 |
|
|
1299 |
Let f be a non-negative function defined on the interval [0, 1]. If and f(0) = 0, then a) b) c) d)
Let f be a non-negative function defined on the interval [0, 1]. If and f(0) = 0, then a) b) c) d)
|
IIT 2009 |
|
|
1300 |
(One or more correct answers)
If E and F are independent events such that 0 < P (E) < 1 and 0 < P (F) < 1 then a) E and F are mutually exclusive b) E and 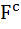 are independent are independent c) 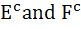 are independent are independent d) 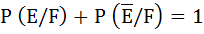
(One or more correct answers)
If E and F are independent events such that 0 < P (E) < 1 and 0 < P (F) < 1 then a) E and F are mutually exclusive b) E and 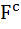 are independent are independent c) 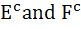 are independent are independent d) 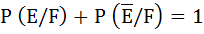
|
IIT 1989 |
|