|
1251 |
Multiple choices Let 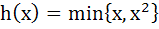 for every real number x then for every real number x then a) h (x) is continuous for all x b) h is differentiable for all x c) 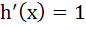 for all x > 1 for all x > 1 d) h is not differentiable for two values of x
Multiple choices Let 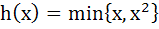 for every real number x then for every real number x then a) h (x) is continuous for all x b) h is differentiable for all x c) 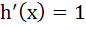 for all x > 1 for all x > 1 d) h is not differentiable for two values of x
|
IIT 1998 |
|
|
1252 |
Number of divisors of the form 4n + 2(n ≥ 0) of integer 240 is a) 4 b) 8 c) 10 d) 3
Number of divisors of the form 4n + 2(n ≥ 0) of integer 240 is a) 4 b) 8 c) 10 d) 3
|
IIT 1998 |
|
|
1253 |
The smallest positive root of the equation tan x – x = 0 lies in a) 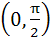 b) 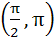 c) 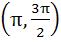 d) 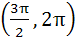 e) None of these
The smallest positive root of the equation tan x – x = 0 lies in a) 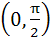 b) 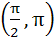 c) 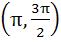 d) 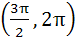 e) None of these
|
IIT 1987 |
|
|
1254 |
Let f (x) be defined on the interval 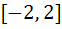 such that such that 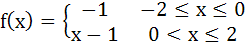
g (x) = f (|x|) + |f(x)| Test the differentiability of g (x) in 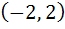 a) g(x) is differentiable at all x  ℝ ℝ b) g(x) is differentiable at all x 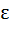 ℝ except at x = 1 ℝ except at x = 1 c) g(x) is differentiable at all x 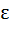 ℝ except at x = 0, 1 ℝ except at x = 0, 1 d) g(x) is differentiable at all x 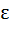 ℝ except at x = 0, 1, 2 ℝ except at x = 0, 1, 2
Let f (x) be defined on the interval 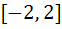 such that such that 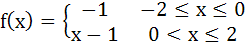
g (x) = f (|x|) + |f(x)| Test the differentiability of g (x) in 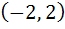 a) g(x) is differentiable at all x 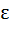 ℝ ℝ b) g(x) is differentiable at all x 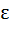 ℝ except at x = 1 ℝ except at x = 1 c) g(x) is differentiable at all x 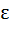 ℝ except at x = 0, 1 ℝ except at x = 0, 1 d) g(x) is differentiable at all x 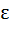 ℝ except at x = 0, 1, 2 ℝ except at x = 0, 1, 2
|
IIT 1986 |
|
|
1255 |
If the LCM of p, q is 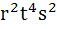 where r, s, t are prime numbers and p, q are positive integers then the number of ordered pairs (p, q) is where r, s, t are prime numbers and p, q are positive integers then the number of ordered pairs (p, q) is a) 252 b) 254 c) 225 d) 224
If the LCM of p, q is 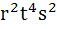 where r, s, t are prime numbers and p, q are positive integers then the number of ordered pairs (p, q) is where r, s, t are prime numbers and p, q are positive integers then the number of ordered pairs (p, q) is a) 252 b) 254 c) 225 d) 224
|
IIT 2006 |
|
|
1256 |
Consider a family of circles passing through two fixed points A (3, 7) and B (6, 5). Show that the chords in which the circle 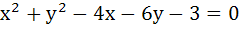 cuts the members of the family are concurrent at a point. Find the coordinates of this point. cuts the members of the family are concurrent at a point. Find the coordinates of this point.
Consider a family of circles passing through two fixed points A (3, 7) and B (6, 5). Show that the chords in which the circle 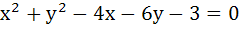 cuts the members of the family are concurrent at a point. Find the coordinates of this point. cuts the members of the family are concurrent at a point. Find the coordinates of this point.
|
IIT 1993 |
|
|
1257 |
In how many ways can a pack of 52 cards be divided into four groups of 13 cards each.
In how many ways can a pack of 52 cards be divided into four groups of 13 cards each.
|
IIT 1979 |
|
|
1258 |
In a triangle ABC, let ∠ C = 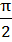 . If r is the inradius and R is the circumradius of the triangle then 2(r+R) = …………. . If r is the inradius and R is the circumradius of the triangle then 2(r+R) = …………. a) a+b b) b+c c) c+a d) a+b+c
In a triangle ABC, let ∠ C = 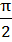 . If r is the inradius and R is the circumradius of the triangle then 2(r+R) = …………. . If r is the inradius and R is the circumradius of the triangle then 2(r+R) = …………. a) a+b b) b+c c) c+a d) a+b+c
|
IIT 2000 |
|
|
1259 |
Determine the values of x for which the following function fails to be continuous or differentiable. 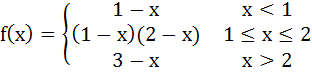
Justify your answer. a) f(x) is continuous and differentiable b) f(x) is continuous everywhere but not differentiable at
x = 1, 2 c) f(x) is continuous everywhere but not differentiable at x = 2 d) f(x) is neither continuous nor differentiable at x = 1, 2
Determine the values of x for which the following function fails to be continuous or differentiable. 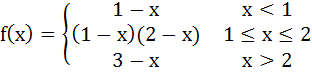
Justify your answer. a) f(x) is continuous and differentiable b) f(x) is continuous everywhere but not differentiable at
x = 1, 2 c) f(x) is continuous everywhere but not differentiable at x = 2 d) f(x) is neither continuous nor differentiable at x = 1, 2
|
IIT 1997 |
|
|
1260 |
Let 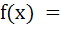 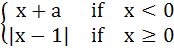 And 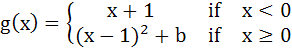 where a and b are non-negative real numbers. Determine the composite function gof. If (gof)(x) is continuous for all real x, determine the values of a and b. Is gof differentiable at x = 0? a) a = b = 0 b) a = 0, b = 1 c) a = 1, b = 0 d) a = b = 1
Let 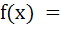 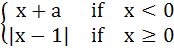 And 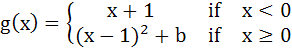 where a and b are non-negative real numbers. Determine the composite function gof. If (gof)(x) is continuous for all real x, determine the values of a and b. Is gof differentiable at x = 0? a) a = b = 0 b) a = 0, b = 1 c) a = 1, b = 0 d) a = b = 1
|
IIT 2002 |
|
|
1261 |
Find the equation of the circle touching the line 2x + 3y + 1 = 0 at the point (1, −1) and is orthogonal to the circle which has the line segment having end points (0, −1) and (−2, 3) as diameter.
Find the equation of the circle touching the line 2x + 3y + 1 = 0 at the point (1, −1) and is orthogonal to the circle which has the line segment having end points (0, −1) and (−2, 3) as diameter.
|
IIT 2004 |
|
|
1262 |
Show that the value of 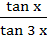 wherever defined wherever defined a) always lies between  and 3 and 3 b) never lies between  and 3 and 3 c) depends on the value of x
Show that the value of 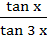 wherever defined wherever defined a) always lies between  and 3 and 3 b) never lies between  and 3 and 3 c) depends on the value of x
|
IIT 1992 |
|
|
1263 |
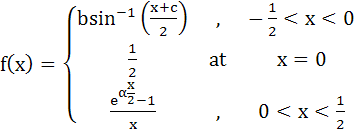
Show that f(x) is differentiable at the value of α = 1. Also, a) b2 +c2 = 4 b) 4 b2 = 4 − c2 c) 64 b2 = 4 − c2 d) 64 b2 = 4 + c2
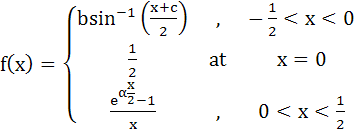
Show that f(x) is differentiable at the value of α = 1. Also, a) b2 +c2 = 4 b) 4 b2 = 4 − c2 c) 64 b2 = 4 − c2 d) 64 b2 = 4 + c2
|
IIT 2004 |
|
|
1264 |
The product of r consecutive natural numbers is divisible by r! a) True b) False
The product of r consecutive natural numbers is divisible by r! a) True b) False
|
IIT 1985 |
|
|
1265 |
The area bounded by the curve y = f(x), the X–axis and the ordinates x = 1, x = b is (b – 1) sin (3b + 4). Then f(x) is a) (x – 1) cos (3x + b) b) sin (3x + 4) c) sin (3x + 4) + 3 (x – 1) cos (3x + 4) d) none of these
The area bounded by the curve y = f(x), the X–axis and the ordinates x = 1, x = b is (b – 1) sin (3b + 4). Then f(x) is a) (x – 1) cos (3x + b) b) sin (3x + 4) c) sin (3x + 4) + 3 (x – 1) cos (3x + 4) d) none of these
|
IIT 2005 |
|
|
1266 |
The sum 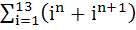 where where 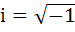 equals equals a) i b) i – 1 c) – i d) 0
The sum 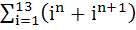 where where 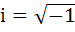 equals equals a) i b) i – 1 c) – i d) 0
|
IIT 1998 |
|
|
1267 |
Fill in the blank The value of f (x) = 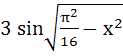 lies in the interval ……………. lies in the interval ……………. a) 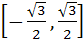 b) 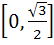 c) 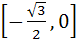 d) 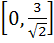
Fill in the blank The value of f (x) = 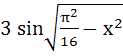 lies in the interval ……………. lies in the interval ……………. a) 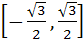 b) 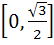 c) 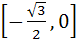 d) 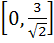
|
IIT 1983 |
|
|
1268 |
Find the area bounded by the curve x2 = 4y and the straight line
x = 4y – 2. a) 3/2 b) 3/4 c) 9/4 d) 9/8
Find the area bounded by the curve x2 = 4y and the straight line
x = 4y – 2. a) 3/2 b) 3/4 c) 9/4 d) 9/8
|
IIT 1981 |
|
|
1269 |
If f(x) and g(x) are differentiable functions for 0 ≤ x ≤ 1 such that f(0) = 2, g(0) = 0, f(1) = 6, g(1) = 2 then show that there exists c satisfying 0 < c < 1 and 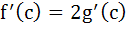 . . a) 0 < c < 1 and 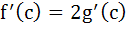 b) 0 < c < 1 and 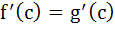 c) 0 < c < 1 and 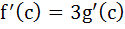 d) 0 < c < 1 and 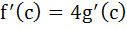
If f(x) and g(x) are differentiable functions for 0 ≤ x ≤ 1 such that f(0) = 2, g(0) = 0, f(1) = 6, g(1) = 2 then show that there exists c satisfying 0 < c < 1 and 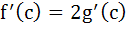 . . a) 0 < c < 1 and 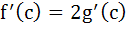 b) 0 < c < 1 and 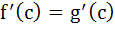 c) 0 < c < 1 and 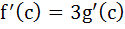 d) 0 < c < 1 and 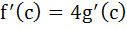
|
IIT 1982 |
|
|
1270 |
Let a > 0, b > 0, c > 0 then both the roots of the equation 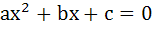 a) are real and positive b) have negative real parts c) have positive real parts d) none of these
Let a > 0, b > 0, c > 0 then both the roots of the equation 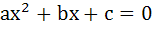 a) are real and positive b) have negative real parts c) have positive real parts d) none of these
|
IIT 1979 |
|
|
1271 |
If f(x) is a continuous function defined for 1 ≤ x ≤ 3. If f(x) takes rational values for all x and f(2) = 10 then f(1.5) = . . . . a) 2 b) 5 c) 10 d) 20
If f(x) is a continuous function defined for 1 ≤ x ≤ 3. If f(x) takes rational values for all x and f(2) = 10 then f(1.5) = . . . . a) 2 b) 5 c) 10 d) 20
|
IIT 1997 |
|
|
1272 |
If x, y, z are real and distinct then 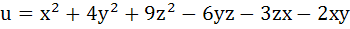 is always is always a) Non – negative b) Non – positive c) Zero d) None of these
If x, y, z are real and distinct then 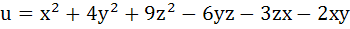 is always is always a) Non – negative b) Non – positive c) Zero d) None of these
|
IIT 2005 |
|
|
1273 |
Match the following
Let [x] denote the greatest integer less than or equal to x | Column 1 | Column 2 | | i) x|x| | A)continuous in 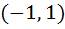 | | ii) 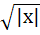 | B)Differentiable in 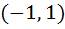 | | iii) x + [x] | C)Steadily increasing in 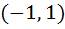 | | iv) |x – 1| + |x + 1| | D) Not differentiable at least at one point in 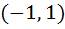 | a) (i)→ A, B, C, (ii)→ A, D, (iii)→ C, D, (iv)→ A, B b) (i)→ A, (ii)→ A, (iii)→ C, (iv)→ B c) (i)→ B, (ii)→ D, (iii)→ C, (iv)→ A d) (i)→ A, B, (ii)→ A, D, (iii)→ C, D, (iv)→ B
Match the following
Let [x] denote the greatest integer less than or equal to x | Column 1 | Column 2 | | i) x|x| | A)continuous in 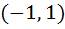 | | ii) 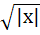 | B)Differentiable in 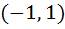 | | iii) x + [x] | C)Steadily increasing in 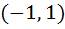 | | iv) |x – 1| + |x + 1| | D) Not differentiable at least at one point in 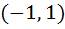 | a) (i)→ A, B, C, (ii)→ A, D, (iii)→ C, D, (iv)→ A, B b) (i)→ A, (ii)→ A, (iii)→ C, (iv)→ B c) (i)→ B, (ii)→ D, (iii)→ C, (iv)→ A d) (i)→ A, B, (ii)→ A, D, (iii)→ C, D, (iv)→ B
|
IIT 2007 |
|
|
1274 |
(One or more than one correct answer)
If 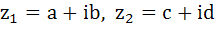 are complex numbers such that are complex numbers such that 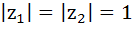 and and 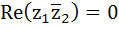 then the pair of complex numbers then the pair of complex numbers 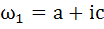 and and 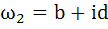 satisfy satisfy a) 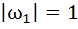 b) 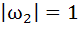 c) 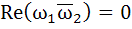 d) None of these
|
IIT 1985 |
|
|
1275 |
Let ABCD be a square with side of length 2 units. C2 is the circle through the vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. A line M is drawn through A parallel to BD. Point S moves such that the distance from the line BD and the vertex A are equal. If the locus of S cuts M at T2 and T3 and AC at T1, then find the area of △T1T2T3.
Let ABCD be a square with side of length 2 units. C2 is the circle through the vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. A line M is drawn through A parallel to BD. Point S moves such that the distance from the line BD and the vertex A are equal. If the locus of S cuts M at T2 and T3 and AC at T1, then find the area of △T1T2T3.
|
IIT 2006 |
|