|
1176 |
Let T1, T2 be two tangents drawn from (−2, 0) onto the circle C: x2 + y2 = 1. Determine the circle touching C and having T1, T2 as their pair of tangents. Further find the equation of all possible common tangents to the circles, when taken two at a time.
Let T1, T2 be two tangents drawn from (−2, 0) onto the circle C: x2 + y2 = 1. Determine the circle touching C and having T1, T2 as their pair of tangents. Further find the equation of all possible common tangents to the circles, when taken two at a time.
|
IIT 1999 |
|
|
1177 |
Let 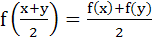 for all real x and y. If for all real x and y. If 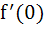 exists and exists and 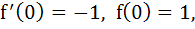 then find f(2) then find f(2) a) – 1 b) 0 c) 1 d) 2
Let 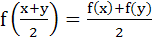 for all real x and y. If for all real x and y. If 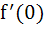 exists and exists and 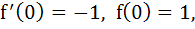 then find f(2) then find f(2) a) – 1 b) 0 c) 1 d) 2
|
IIT 1995 |
|
|
1178 |
Let 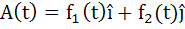 and and 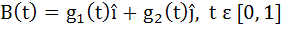 where where 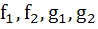 are continuous functions. If A(t) and B(t) are non-zero vectors for all t and are continuous functions. If A(t) and B(t) are non-zero vectors for all t and A(0) = 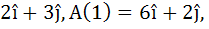 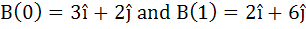
then A(t) and b(t) are parallel for some t. a) True b) False
Let 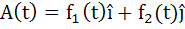 and and 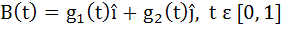 where where 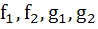 are continuous functions. If A(t) and B(t) are non-zero vectors for all t and are continuous functions. If A(t) and B(t) are non-zero vectors for all t and A(0) = 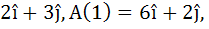 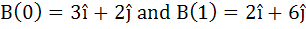
then A(t) and b(t) are parallel for some t. a) True b) False
|
IIT 2001 |
|
|
1179 |
Let n be any positive integer. Prove that 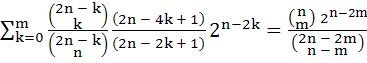
For each non negative integer m ≤ n
Let n be any positive integer. Prove that 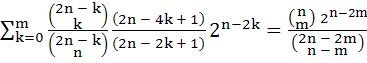
For each non negative integer m ≤ n
|
IIT 1999 |
|
|
1180 |
Find the centre and radius of the circle formed by all the points represented by 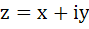 satisfying the relation satisfying the relation 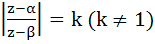 where α and β are complex numbers given by where α and β are complex numbers given by
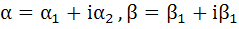
|
IIT 2004 |
|
|
1181 |
Using permutation or otherwise prove that 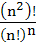 is an integer, where n is a positive integer. is an integer, where n is a positive integer.
Using permutation or otherwise prove that 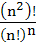 is an integer, where n is a positive integer. is an integer, where n is a positive integer.
|
IIT 2004 |
|
|
1182 |
Three circles of radii 3, 4 and 5 units touch each other externally and tangents drawn at the points of contact intersect at P. Find the distance between P and the point of contact.
Three circles of radii 3, 4 and 5 units touch each other externally and tangents drawn at the points of contact intersect at P. Find the distance between P and the point of contact.
|
IIT 2005 |
|
|
1183 |
In ΔABC, D is the midpoint of BC. If AD is perpendicular to AC then 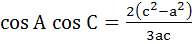 . . a) True b) False
In ΔABC, D is the midpoint of BC. If AD is perpendicular to AC then 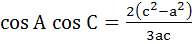 . . a) True b) False
|
IIT 1980 |
|
|
1184 |
A function f : R  R where R is the set of real numbers is defined by f (x) = R where R is the set of real numbers is defined by f (x) = 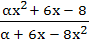 . Find the interval of values of α for which f is onto. Is the function one to one for α = 3? Justify your answer. . Find the interval of values of α for which f is onto. Is the function one to one for α = 3? Justify your answer. a) 2 ≤ α ≤ 14 b) α ≥ 2 c) α ≤ 14 d) none of the above
A function f : R  R where R is the set of real numbers is defined by f (x) = R where R is the set of real numbers is defined by f (x) = 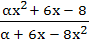 . Find the interval of values of α for which f is onto. Is the function one to one for α = 3? Justify your answer. . Find the interval of values of α for which f is onto. Is the function one to one for α = 3? Justify your answer. a) 2 ≤ α ≤ 14 b) α ≥ 2 c) α ≤ 14 d) none of the above
|
IIT 1996 |
|
|
1185 |
If f1 ( x ) and f2 ( x ) are defined by domains D1 and D2 respectively, then f1 ( x ) + f2 ( x ) is defined as on D1 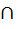 D2. D2. a) True b) False
If f1 ( x ) and f2 ( x ) are defined by domains D1 and D2 respectively, then f1 ( x ) + f2 ( x ) is defined as on D1 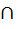 D2. D2. a) True b) False
|
IIT 1988 |
|
|
1186 |
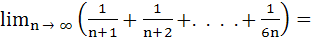
a) ln2 b) ln3 c) ln6 d) ln2 ln3
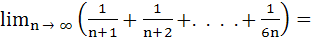
a) ln2 b) ln3 c) ln6 d) ln2 ln3
|
IIT 1980 |
|
|
1187 |
For all complex numbers satisfying 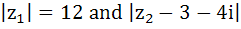 = 5, the minimum value of = 5, the minimum value of 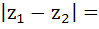 a) 0 b) 2 c) 7 d) 17
For all complex numbers satisfying 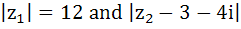 = 5, the minimum value of = 5, the minimum value of 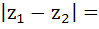 a) 0 b) 2 c) 7 d) 17
|
IIT 2002 |
|
|
1188 |
Use the function 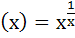 , x > 0 to determine the bigger of the numbers eπ and πe. , x > 0 to determine the bigger of the numbers eπ and πe. a) eπ b) πe
Use the function 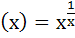 , x > 0 to determine the bigger of the numbers eπ and πe. , x > 0 to determine the bigger of the numbers eπ and πe. a) eπ b) πe
|
IIT 1981 |
|
|
1189 |
In a triangle ABC, D and E are points on 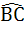 and and 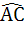 respectively such that respectively such that 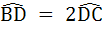 and and 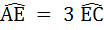 . Let P be the point of intersection of . Let P be the point of intersection of 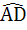 and and 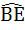 . Find . Find 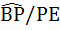 using vector method. using vector method. a)  b)  c)  d) 2
|
IIT 1993 |
|
|
1190 |
The minimum value of 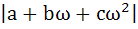 where a, b c are all not equal integers and ω(≠1) a cube root of unity is where a, b c are all not equal integers and ω(≠1) a cube root of unity is a) 1 b) 0 c) 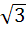 d) 
The minimum value of 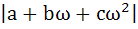 where a, b c are all not equal integers and ω(≠1) a cube root of unity is where a, b c are all not equal integers and ω(≠1) a cube root of unity is a) 1 b) 0 c) 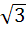 d) 
|
IIT 2005 |
|
|
1191 |
Match the following
Let the functions defined in column 1 have domain 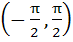
| Column 1 | Column 2 | | i) sin(π[x]) | A) differentiable everywhere | | ii) sinπ(x-[x]) | B) nowhere differentiable | | | C) not differentiable at 1,  1 1 | a) i) → A, ii) → B b) i) → A, ii) → C c) i) → C, ii) → A d) i) → B, ii) → C
Match the following
Let the functions defined in column 1 have domain 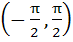
| Column 1 | Column 2 | | i) sin(π[x]) | A) differentiable everywhere | | ii) sinπ(x-[x]) | B) nowhere differentiable | | | C) not differentiable at 1, 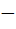 1 1 | a) i) → A, ii) → B b) i) → A, ii) → C c) i) → C, ii) → A d) i) → B, ii) → C
|
IIT 1992 |
|
|
1192 |
Find the area of the region bounded by the X–axis and the curve defined by
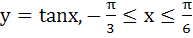
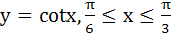 a) ln2 b) 2ln2 c) 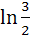 d) 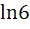
Find the area of the region bounded by the X–axis and the curve defined by
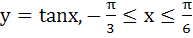
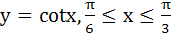 a) ln2 b) 2ln2 c) 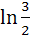 d) 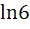
|
IIT 1984 |
|
|
1193 |
Let ABCD be a square with side of length 2 units. C2 is the circle through the vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. A circle touching the line L and the circle C1 externally such that both the circles are on the same side of the line, then the locus of the centre of circle is a) Ellipse b) Hyperbola c) Parabola d) Pair of straight lines
Let ABCD be a square with side of length 2 units. C2 is the circle through the vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. A circle touching the line L and the circle C1 externally such that both the circles are on the same side of the line, then the locus of the centre of circle is a) Ellipse b) Hyperbola c) Parabola d) Pair of straight lines
|
IIT 2006 |
|
|
1194 |
Find three dimensional vectors u1, u2, u3 satisfying
u1.u1 = 4; u1.u2 = −2; u1.u3 = 6; u2.u2 = 2; u2.u3 = −5; u3.u3 = 29
Find three dimensional vectors u1, u2, u3 satisfying
u1.u1 = 4; u1.u2 = −2; u1.u3 = 6; u2.u2 = 2; u2.u3 = −5; u3.u3 = 29
|
IIT 2001 |
|
|
1195 |
If a continuous function f defined on the real line ℝ, assumes positive and negative values in ℝ then the equation f(x) = 0 has a root in ℝ. For example, it is known that if a continuous function f on ℝ is positive at some points and its minimum value is negative then the equation f(x) = 0 has a root in ℝ. Consider the function f(x) = 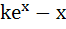 for all real x where k is a real constant. for all real x where k is a real constant. For k > 0, the set of all values of k for which 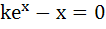 has two distinct roots is has two distinct roots is a) 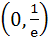 b) 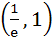 c) 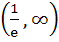 d) (0, 1)
If a continuous function f defined on the real line ℝ, assumes positive and negative values in ℝ then the equation f(x) = 0 has a root in ℝ. For example, it is known that if a continuous function f on ℝ is positive at some points and its minimum value is negative then the equation f(x) = 0 has a root in ℝ. Consider the function f(x) = 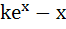 for all real x where k is a real constant. for all real x where k is a real constant. For k > 0, the set of all values of k for which 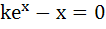 has two distinct roots is has two distinct roots is a) 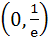 b) 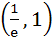 c) 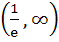 d) (0, 1)
|
IIT 2007 |
|
|
1196 |
Let f(x) = x3 – x2 + x + 1 and
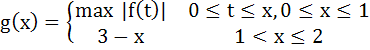
Discuss the continuity and differentiability of f(x) in the interval (0, 2) a) Continuous and differentiable in (0, 2) b) Continuous and differentiable in (0, 2)except x = 1 c) Continuous in (0, 2). Differentiable in (0, 2) except x = 1 d) None of the above
Let f(x) = x3 – x2 + x + 1 and
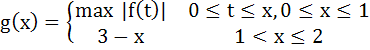
Discuss the continuity and differentiability of f(x) in the interval (0, 2) a) Continuous and differentiable in (0, 2) b) Continuous and differentiable in (0, 2)except x = 1 c) Continuous in (0, 2). Differentiable in (0, 2) except x = 1 d) None of the above
|
IIT 1985 |
|
|
1197 |
A relation R on the set of complex numbers is defined by 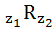 iff iff 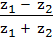 is real. Show that R is an equivalence relation. is real. Show that R is an equivalence relation.
A relation R on the set of complex numbers is defined by 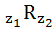 iff iff 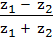 is real. Show that R is an equivalence relation. is real. Show that R is an equivalence relation.
|
IIT 1982 |
|
|
1198 |
Find the point on the curve 4x2 + a2y2 = 4a2, 4 < a2 < 8 that is farthest from the point (0, −2). a) (a, 0) b) 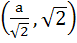 c) 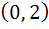 d) (0, - 2)
Find the point on the curve 4x2 + a2y2 = 4a2, 4 < a2 < 8 that is farthest from the point (0, −2). a) (a, 0) b) 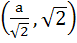 c) 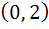 d) (0, - 2)
|
IIT 1987 |
|
|
1199 |
The locus of the mid-point of the line segment joining the focus to a moving point on the parabola y2 = 4ax is another parabola with directrix a) x = −a b) 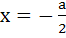 c) 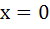 d) 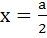
The locus of the mid-point of the line segment joining the focus to a moving point on the parabola y2 = 4ax is another parabola with directrix a) x = −a b) 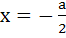 c) 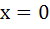 d) 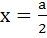
|
IIT 2002 |
|
|
1200 |
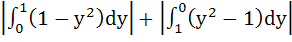
|
IIT 2006 |
|