|
1101 |
If x is not an integral multiple of 2π use mathematical induction to prove that
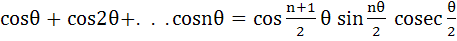
If x is not an integral multiple of 2π use mathematical induction to prove that
|
IIT 1994 |
|
|
1102 |
A circle passing through (1, −2) and touching the axis of X at (3, 0) also passes through the point a) (−5, 2) b) (2, −5) c) (5, −2) d) (−2, 5)
A circle passing through (1, −2) and touching the axis of X at (3, 0) also passes through the point a) (−5, 2) b) (2, −5) c) (5, −2) d) (−2, 5)
|
IIT 2013 |
|
|
1103 |
The circles 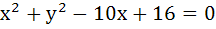 and and 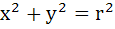 intersect each other in distinct points if intersect each other in distinct points if a) r < 2 b) r > 8 c) 2 < r < 8 d) 2 ≤ r ≤ 8
The circles 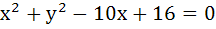 and and 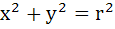 intersect each other in distinct points if intersect each other in distinct points if a) r < 2 b) r > 8 c) 2 < r < 8 d) 2 ≤ r ≤ 8
|
IIT 1994 |
|
|
1104 |
Prove by induction that
Pn = Aαn + Bβn for all n ≥ 1
Where α and β are roots of the quadratic equation
x2 – (1 – P) x – P (1 – P) = 0,
P1 = 1, P2 = 1 – P2, . . .,
Pn = (1 – P) Pn – 1 + P (1 – P) Pn – 2 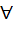 n ≥ 3, n ≥ 3,
and  , , 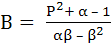
|
IIT 2000 |
|
|
1105 |
Let P be a point on the parabola y2 = 8x which is at a minimum distance from the centre C of the circle x2 + (y + 6)2 = 1. Then the equation of the circle passing through C and having its centre at P is a) x2 + y2 – 4x + 8y + 12 = 0 b) x2 + y2 –x + 4y − 12 = 0 c) x2 + y2 –x + 2y − 24 = 0 d) x2 + y2 – 4x + 9y + 18 = 0
Let P be a point on the parabola y2 = 8x which is at a minimum distance from the centre C of the circle x2 + (y + 6)2 = 1. Then the equation of the circle passing through C and having its centre at P is a) x2 + y2 – 4x + 8y + 12 = 0 b) x2 + y2 –x + 4y − 12 = 0 c) x2 + y2 –x + 2y − 24 = 0 d) x2 + y2 – 4x + 9y + 18 = 0
|
IIT 2016 |
|
|
1106 |
Let 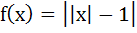 then points where f (x) is not differentiable is (are) then points where f (x) is not differentiable is (are) a) 0 b) 1 c) ± 1 d) 0, ± 1
Let 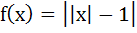 then points where f (x) is not differentiable is (are) then points where f (x) is not differentiable is (are) a) 0 b) 1 c) ± 1 d) 0, ± 1
|
IIT 2005 |
|
|
1107 |
The slope of the line touching both parabolas y2 = 4x and x2 = −32y is a) b) c) d)
The slope of the line touching both parabolas y2 = 4x and x2 = −32y is a) b) c) d)
|
IIT 2014 |
|
|
1108 |
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and QR intersect at a point x on the circumference of the circle, then 2r equals a) 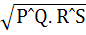 b) 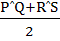 c) 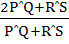 d) 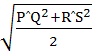
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and QR intersect at a point x on the circumference of the circle, then 2r equals a) 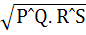 b) 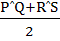 c) 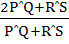 d) 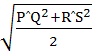
|
IIT 2001 |
|
|
1109 |
Multiple choices Let [x] denote the greatest integer less than or equal to x. If f (x) = [xsinπx] then f(x) is a) Continuous at x = 0 b) Continuous in 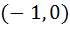 c) f (x) is differentiable at x = 1 d) differentiable in 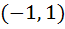 e) None of these
Multiple choices Let [x] denote the greatest integer less than or equal to x. If f (x) = [xsinπx] then f(x) is a) Continuous at x = 0 b) Continuous in 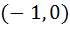 c) f (x) is differentiable at x = 1 d) differentiable in 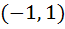 e) None of these
|
IIT 1986 |
|
|
1110 |
Let 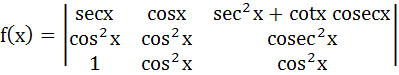 then then 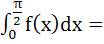 a) 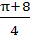 b) 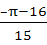 c) 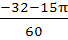 d) 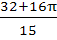
|
IIT 1987 |
|
|
1111 |
Let a, r, s, t be non-zero real numbers. Let P(at2, 2at), Q, R(ar2, 2ar and S(as2, 2as) be distinct points on the parabola y2 = 4ax. Suppose PQ is the focal chord and QR and PK are parallel, where K is point (2a, 0) The value of r is a) b) c) d)
Let a, r, s, t be non-zero real numbers. Let P(at2, 2at), Q, R(ar2, 2ar and S(as2, 2as) be distinct points on the parabola y2 = 4ax. Suppose PQ is the focal chord and QR and PK are parallel, where K is point (2a, 0) The value of r is a) b) c) d)
|
IIT 2014 |
|
|
1112 |
Find all solutions of 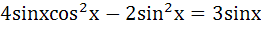 a) 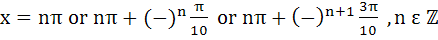 b) 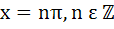 c) 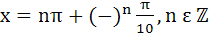 d) 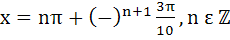
Find all solutions of 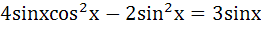 a) 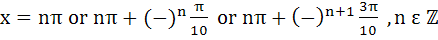 b) 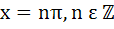 c) 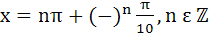 d) 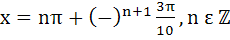
|
IIT 1983 |
|
|
1113 |
Multiple choices Which of the following functions are continuous on (0, π) a) tanx b) 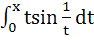 c) 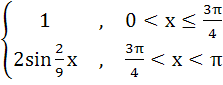 d) 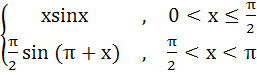
Multiple choices Which of the following functions are continuous on (0, π) a) tanx b) 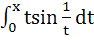 c) 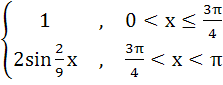 d) 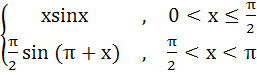
|
IIT 1991 |
|
|
1114 |
One or more than one correct option If the normals of the parabola y2 = 4x drawn at the end points of the latus rectum are tangents to the circle (x − 3)2 + (y + 2)2 = r2 then the value of r2 is a) 4 b) 1 c) 2 d) 0
One or more than one correct option If the normals of the parabola y2 = 4x drawn at the end points of the latus rectum are tangents to the circle (x − 3)2 + (y + 2)2 = r2 then the value of r2 is a) 4 b) 1 c) 2 d) 0
|
IIT 2015 |
|
|
1115 |
Multiple choices Let 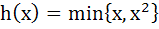 for every real number x then for every real number x then a) h (x) is continuous for all x b) h is differentiable for all x c) 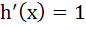 for all x > 1 for all x > 1 d) h is not differentiable for two values of x
Multiple choices Let 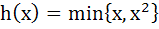 for every real number x then for every real number x then a) h (x) is continuous for all x b) h is differentiable for all x c) 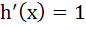 for all x > 1 for all x > 1 d) h is not differentiable for two values of x
|
IIT 1998 |
|
|
1116 |
Let f and g be increasing and decreasing functions, respectively from [0, ∞) to [0, ∞). Let h(x) =f(g(x)). If h(0) = 0 then h(x) – h(t) is a) Always zero b) Always negative c) Always positive d) Strictly increasing e) None of these
Let f and g be increasing and decreasing functions, respectively from [0, ∞) to [0, ∞). Let h(x) =f(g(x)). If h(0) = 0 then h(x) – h(t) is a) Always zero b) Always negative c) Always positive d) Strictly increasing e) None of these
|
IIT 1988 |
|
|
1117 |
Let E = {1, 2, 3, 4} and F = {1, 2} then the number of onto functions from E to F is a) 14 b) 16 c) 12 d) 8
Let E = {1, 2, 3, 4} and F = {1, 2} then the number of onto functions from E to F is a) 14 b) 16 c) 12 d) 8
|
IIT 2001 |
|
|
1118 |
On the interval [0, 1] the function 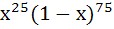 takes the maximum value at the point takes the maximum value at the point a) 0 b)  c)  d) 
On the interval [0, 1] the function 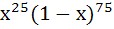 takes the maximum value at the point takes the maximum value at the point a) 0 b)  c)  d) 
|
IIT 1995 |
|
|
1119 |
Let f (x) be continuous and g (x) be a discontinuous function. Prove that f (x) + g (x) is a discontinuous function. a) True b) False c) Could be continuous or discontinuous
Let f (x) be continuous and g (x) be a discontinuous function. Prove that f (x) + g (x) is a discontinuous function. a) True b) False c) Could be continuous or discontinuous
|
IIT 1987 |
|
|
1120 |
Find the coordinates of the point at which the circles x2 + y2 – 4x – 2y = – 4 and x2 + y2 – 12x – 8y = – 36 touch each other. Also find the equation of the common tangents touching the circles at distinct points.
Find the coordinates of the point at which the circles x2 + y2 – 4x – 2y = – 4 and x2 + y2 – 12x – 8y = – 36 touch each other. Also find the equation of the common tangents touching the circles at distinct points.
|
IIT 1993 |
|
|
1121 |
Draw the graph of the function y = [x] + |1 – x|, – 1 ≤ x ≤ 3. Determine the points, if any, where the function is not differentiable. a) y is differentiable everywhere b) y is not differentiable at x = 0 c) y is not differentiable at x = 0, 1, 2 d) y is not differentiable at x = 0, 1, 2 and 3
Draw the graph of the function y = [x] + |1 – x|, – 1 ≤ x ≤ 3. Determine the points, if any, where the function is not differentiable. a) y is differentiable everywhere b) y is not differentiable at x = 0 c) y is not differentiable at x = 0, 1, 2 d) y is not differentiable at x = 0, 1, 2 and 3
|
IIT 1989 |
|
|
1122 |
In how many ways can a pack of 52 cards be divided in 4 sets, three of them having 17 cards each and fourth just one card.
In how many ways can a pack of 52 cards be divided in 4 sets, three of them having 17 cards each and fourth just one card.
|
IIT 1979 |
|
|
1123 |
The area bounded by the curves 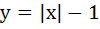 and and 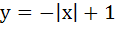 is is
a) 1 b) 2 c) 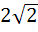 d) 4
The area bounded by the curves 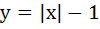 and and 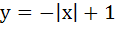 is is
a) 1 b) 2 c) 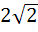 d) 4
|
IIT 2002 |
|
|
1124 |
Let ABC be an equilateral triangle inscribed in the circle x2 + y2 = a2. Suppose perpendiculars from A, B, C to the major axis of the ellipse 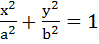 (a > b) meet the ellipse respectively at P, Q, R so that P, Q, R are on the same side of the major axis. Prove that the normals drawn at the points P, Q and R are concurrent. (a > b) meet the ellipse respectively at P, Q, R so that P, Q, R are on the same side of the major axis. Prove that the normals drawn at the points P, Q and R are concurrent.
Let ABC be an equilateral triangle inscribed in the circle x2 + y2 = a2. Suppose perpendiculars from A, B, C to the major axis of the ellipse 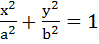 (a > b) meet the ellipse respectively at P, Q, R so that P, Q, R are on the same side of the major axis. Prove that the normals drawn at the points P, Q and R are concurrent. (a > b) meet the ellipse respectively at P, Q, R so that P, Q, R are on the same side of the major axis. Prove that the normals drawn at the points P, Q and R are concurrent.
|
IIT 2000 |
|
|
1125 |
Which of the following pieces of data does not uniquely determine an acute angled triangle ABC (R being the radius of the circumcircle). a) a, sinA, sinB b) a, b , c c) a, sinB, R d) a, sinA, R
Which of the following pieces of data does not uniquely determine an acute angled triangle ABC (R being the radius of the circumcircle). a) a, sinA, sinB b) a, b , c c) a, sinB, R d) a, sinA, R
|
IIT 2002 |
|