|
1076 |
Prove that 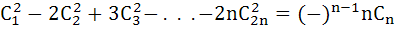
Prove that 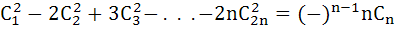
|
IIT 1979 |
|
|
1077 |
The question contains Statement – 1(assertion) and Statement – 2 (reason). Let f (x) = 2 + cosx for all real x. Statement 1: For each real t, there exists a point c in [t, t + π] such that 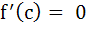 because because Statement 2: f (t) = f[t, t + 2π] for each real t a) Statement 1 and 2 are true. Statement 2 is a correct explanation of Statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation of Statement 1. c) Statement 1 is true and Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
The question contains Statement – 1(assertion) and Statement – 2 (reason). Let f (x) = 2 + cosx for all real x. Statement 1: For each real t, there exists a point c in [t, t + π] such that 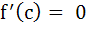 because because Statement 2: f (t) = f[t, t + 2π] for each real t a) Statement 1 and 2 are true. Statement 2 is a correct explanation of Statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation of Statement 1. c) Statement 1 is true and Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2007 |
|
|
1078 |
Let f(x) = (1 – x)2 sin2x + x2 and Which of the following is true? a) g is increasing on (1, ∞) b) g is decreasing on (1, ∞) c) g is increasing on (1, 2) and decreasing on (2, ∞) d) g is decreasing on (1, 2) and increasing on (2, ∞)
Let f(x) = (1 – x)2 sin2x + x2 and Which of the following is true? a) g is increasing on (1, ∞) b) g is decreasing on (1, ∞) c) g is increasing on (1, 2) and decreasing on (2, ∞) d) g is decreasing on (1, 2) and increasing on (2, ∞)
|
IIT 2013 |
|
|
1079 |
Use mathematical induction to prove: If n is an odd positive integer
then 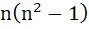 is divisible by 24. is divisible by 24.
Use mathematical induction to prove: If n is an odd positive integer
then 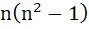 is divisible by 24. is divisible by 24.
|
IIT 1983 |
|
|
1080 |
Let PS is the median of the triangle with vertices P(2, 2), Q(6, −1) and R(7, 3), then the equation of the line passing through (1, −1) and parallel to PS is a) 4x – 7y – 11 = 0 b) 2x + 9y + 7 = 0 c) 4x + 7y + 3 = 0 d) 2x – 9y – 11 = 0
Let PS is the median of the triangle with vertices P(2, 2), Q(6, −1) and R(7, 3), then the equation of the line passing through (1, −1) and parallel to PS is a) 4x – 7y – 11 = 0 b) 2x + 9y + 7 = 0 c) 4x + 7y + 3 = 0 d) 2x – 9y – 11 = 0
|
IIT 2014 |
|
|
1081 |
One or more than one correct option For a > b > c > 0, the distance between (1, 1) and the point of intersection of the lines ax + by + c = 0 and bx + ay + c = 0 is less than , then a) a + b – c > 0 b) a − b + c < 0 c) a − b + c > 0 d) a + b – c < 0
One or more than one correct option For a > b > c > 0, the distance between (1, 1) and the point of intersection of the lines ax + by + c = 0 and bx + ay + c = 0 is less than , then a) a + b – c > 0 b) a − b + c < 0 c) a − b + c > 0 d) a + b – c < 0
|
IIT 2014 |
|
|
1082 |
Using mathematical induction, prove that
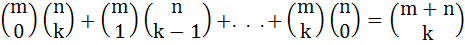
m, n, k are positive integers and 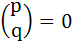 for p < q for p < q
Using mathematical induction, prove that
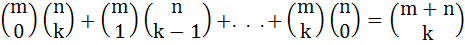
m, n, k are positive integers and 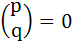 for p < q for p < q
|
IIT 1989 |
|
|
1083 |
If one of the diameters of the circle, given by the equation x2 + y2 – 4x + 6y – 12 = 0 is a chord of a circle S whose centre is at (−3, 2), then the radius of S is a) b) c) d)
If one of the diameters of the circle, given by the equation x2 + y2 – 4x + 6y – 12 = 0 is a chord of a circle S whose centre is at (−3, 2), then the radius of S is a) b) c) d)
|
IIT 2016 |
|
|
1084 |
If 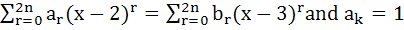 for all k ≥ n then show that for all k ≥ n then show that 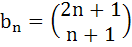
If 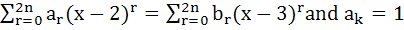 for all k ≥ n then show that for all k ≥ n then show that 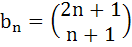
|
IIT 1992 |
|
|
1085 |
The function 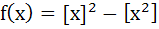 (where [y] is the greatest integer less than or equal to y) is discontinuous at (where [y] is the greatest integer less than or equal to y) is discontinuous at a) All integers b) All integers except 0 and 1 c) All integers except 0 d) All integers except 1
The function 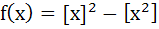 (where [y] is the greatest integer less than or equal to y) is discontinuous at (where [y] is the greatest integer less than or equal to y) is discontinuous at a) All integers b) All integers except 0 and 1 c) All integers except 0 d) All integers except 1
|
IIT 1999 |
|
|
1086 |
If 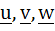 are three non-coplanar unit vectors and α, β, γ are the angles between are three non-coplanar unit vectors and α, β, γ are the angles between 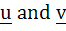 , v and w, w and u respectively and x, y and z are unit vectors along the bisector of the angles α, β, γ respectively. Prove that , v and w, w and u respectively and x, y and z are unit vectors along the bisector of the angles α, β, γ respectively. Prove that
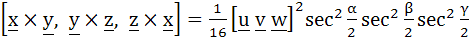
|
IIT 2003 |
|
|
1087 |
For how many values of p, the circlex2 + y2 + 2x + 4y – p = 0 and the coordinate axis have exactly three common points a) 0 b) 1 c) 2 d) 3
For how many values of p, the circlex2 + y2 + 2x + 4y – p = 0 and the coordinate axis have exactly three common points a) 0 b) 1 c) 2 d) 3
|
IIT 2014 |
|
|
1088 |
A tangent PT is drawn to the circle x2 + y2 = 4 at the point . A straight line L, perpendicular to PT is tangent to the circle (x – 3)2 + y2 = 1A common tangent to the circles is a) x = 4 b) y = 2 c) d)
A tangent PT is drawn to the circle x2 + y2 = 4 at the point . A straight line L, perpendicular to PT is tangent to the circle (x – 3)2 + y2 = 1A common tangent to the circles is a) x = 4 b) y = 2 c) d)
|
IIT 2012 |
|
|
1089 |
The integer n, for which 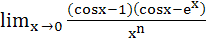 is a finite is a finite non–zero number is a) 1 b) 2 c) 3 d) 4
The integer n, for which 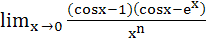 is a finite is a finite non–zero number is a) 1 b) 2 c) 3 d) 4
|
IIT 2002 |
|
|
1090 |
The locus of the middle points of the chord of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is a) 20(x2 + y2) – 36x + 45y = 0 b) 20(x2 + y2) + 36x − 45y = 0 c) 36(x2 + y2) – 20x + 45y = 0 d) 36(x2 + y2) + 20x − 45y = 0
The locus of the middle points of the chord of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is a) 20(x2 + y2) – 36x + 45y = 0 b) 20(x2 + y2) + 36x − 45y = 0 c) 36(x2 + y2) – 20x + 45y = 0 d) 36(x2 + y2) + 20x − 45y = 0
|
IIT 2012 |
|
|
1091 |
Let 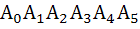 be a regular hexagon in a circle of unit radius. Then the product of the length of the segments be a regular hexagon in a circle of unit radius. Then the product of the length of the segments 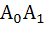 , , 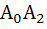 and and 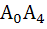 is is a)  b) 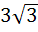 c) 3 d) 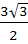
Let 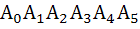 be a regular hexagon in a circle of unit radius. Then the product of the length of the segments be a regular hexagon in a circle of unit radius. Then the product of the length of the segments 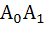 , , 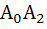 and and 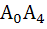 is is a)  b) 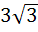 c) 3 d) 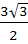
|
IIT 1998 |
|
|
1092 |
f(x) is twice differentiable polynomial function such that f (1) = 1, f (2) = 4, f (3) = 9, then a) there exists at least one x 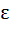 (1, 2) such that (1, 2) such that 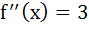 b) there exists at least one x 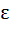 (2, 3) such that (2, 3) such that 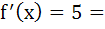 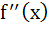 c) 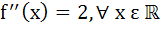 d) there exists at least one x 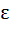 (1, 3) such that (1, 3) such that 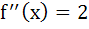
f(x) is twice differentiable polynomial function such that f (1) = 1, f (2) = 4, f (3) = 9, then a) there exists at least one x 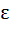 (1, 2) such that (1, 2) such that 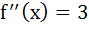 b) there exists at least one x 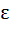 (2, 3) such that (2, 3) such that 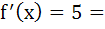 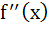 c) 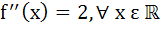 d) there exists at least one x 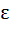 (1, 3) such that (1, 3) such that 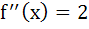
|
IIT 2005 |
|
|
1093 |
The radius of a circle having minimum area which touches the curve y = 4 – x2 and the line y = |x| is a) b) c) d)
The radius of a circle having minimum area which touches the curve y = 4 – x2 and the line y = |x| is a) b) c) d)
|
IIT 2017 |
|
|
1094 |
Let AB be a chord of the circle 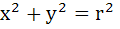 subtending a right angle at the centre then the locus of the centroid of the triangle PAB as P moves on the circle is subtending a right angle at the centre then the locus of the centroid of the triangle PAB as P moves on the circle is a) A parabola b) A circle c) An ellipse d) A pairing straight line
Let AB be a chord of the circle 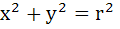 subtending a right angle at the centre then the locus of the centroid of the triangle PAB as P moves on the circle is subtending a right angle at the centre then the locus of the centroid of the triangle PAB as P moves on the circle is a) A parabola b) A circle c) An ellipse d) A pairing straight line
|
IIT 2000 |
|
|
1095 |
Given a circle 2x2 + 2y2 = 5 and a parabola Statement 1: An equation of a common tangent to the curves is Statement 2: If the line is the common tangent then m satisfies m4 – 3m2 + 2 = 0 a) Statement 1 is correct. Statement 2 is correct. Statement 2 is a correct explanation for statement 1 b) Statement 1 is correct. Statement 2 is correct. Statement 2 is not a correct explanation for statement 1 c) Statement 1 is correct. Statement 2 is incorrect. d) Statement 1 is incorrect. Statement 2 is correct.
Given a circle 2x2 + 2y2 = 5 and a parabola Statement 1: An equation of a common tangent to the curves is Statement 2: If the line is the common tangent then m satisfies m4 – 3m2 + 2 = 0 a) Statement 1 is correct. Statement 2 is correct. Statement 2 is a correct explanation for statement 1 b) Statement 1 is correct. Statement 2 is correct. Statement 2 is not a correct explanation for statement 1 c) Statement 1 is correct. Statement 2 is incorrect. d) Statement 1 is incorrect. Statement 2 is correct.
|
IIT 2013 |
|
|
1096 |
One or more than one correct option Let L be a normal to the parabola y2 = 4x. If L passes through the point (9, 6) then L is given by a) y – x + 3 = 0 b) y + 3x – 33 = 0 c) y + x – 15 = 0 d) y – 2x + 12 = 0
One or more than one correct option Let L be a normal to the parabola y2 = 4x. If L passes through the point (9, 6) then L is given by a) y – x + 3 = 0 b) y + 3x – 33 = 0 c) y + x – 15 = 0 d) y – 2x + 12 = 0
|
IIT 2011 |
|
|
1097 |
Let ABCD be a quadrilateral with area 18 with side AB parallel to CD and AB = 2CD. Let AD be perpendicular to AB and CD. A circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is a) 3 b) 2 c)  d) 1
Let ABCD be a quadrilateral with area 18 with side AB parallel to CD and AB = 2CD. Let AD be perpendicular to AB and CD. A circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is a) 3 b) 2 c)  d) 1
|
IIT 2007 |
|
|
1098 |
Multiple choices The function f (x) = max 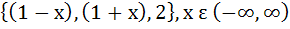 is is a) continuous at all points b) differentiable at all points c) differentiable at all points except x = 1 and x = 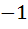 d) continuous at all points except at x=1 and x=-1 where it is discontinuous
Multiple choices The function f (x) = max 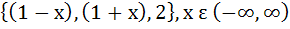 is is a) continuous at all points b) differentiable at all points c) differentiable at all points except x = 1 and x = 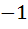 d) continuous at all points except at x=1 and x=-1 where it is discontinuous
|
IIT 1995 |
|
|
1099 |
Find the equation of the circle passing through ( 4, 3) and touching the lines x + y = 4 and 4, 3) and touching the lines x + y = 4 and 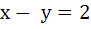 . .
Find the equation of the circle passing through ( 4, 3) and touching the lines x + y = 4 and 4, 3) and touching the lines x + y = 4 and 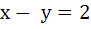 . .
|
IIT 1982 |
|
|
1100 |
A circle touches the line y = x at a point P such that 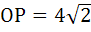 , where O is the origin. The circle contains the point , where O is the origin. The circle contains the point 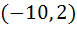 in its interior and the length of its chord on the line in its interior and the length of its chord on the line 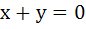 is is 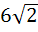 . Determine its equation. . Determine its equation.
|
IIT 1990 |
|