|
1051 |
equals a) 8 b) 2 c) 4 d) 0
equals a) 8 b) 2 c) 4 d) 0
|
IIT 2014 |
|
|
1052 |
Fill in the blank The system of equations
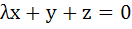
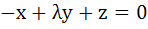
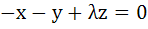
will have a non-zero solution if real value of λ is given by …………
Fill in the blank The system of equations
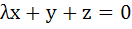
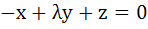
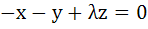
will have a non-zero solution if real value of λ is given by …………
|
IIT 1982 |
|
|
1053 |
The function 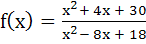 is not one to one is not one to one a) True b) False
The function 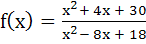 is not one to one is not one to one a) True b) False
|
IIT 1983 |
|
|
1054 |
For any real number x, let [x] denote the greater integer less than or equal to x. Let f be a real valued function defined on the interval [−10, 10] by then the value of is a) 2 b) 0 c) 6 d) 4
For any real number x, let [x] denote the greater integer less than or equal to x. Let f be a real valued function defined on the interval [−10, 10] by then the value of is a) 2 b) 0 c) 6 d) 4
|
IIT 2010 |
|
|
1055 |
Let 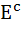 denotes the complement of an event E. Let E, F, G are pair wise independent events with P (G) > 0 and P (E ∩ F ∩ G) = 0 then denotes the complement of an event E. Let E, F, G are pair wise independent events with P (G) > 0 and P (E ∩ F ∩ G) = 0 then 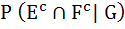 equals equals a) 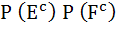 b) 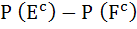 c) 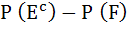 d) 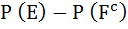
Let 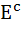 denotes the complement of an event E. Let E, F, G are pair wise independent events with P (G) > 0 and P (E ∩ F ∩ G) = 0 then denotes the complement of an event E. Let E, F, G are pair wise independent events with P (G) > 0 and P (E ∩ F ∩ G) = 0 then 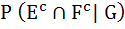 equals equals a) 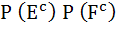 b) 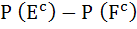 c) 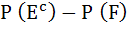 d) 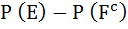
|
IIT 2007 |
|
|
1056 |
Let A be a set of n distinct elements. Then find the total number of distinct functions from A to A is and out of these onto functions are . . .
Let A be a set of n distinct elements. Then find the total number of distinct functions from A to A is and out of these onto functions are . . .
|
IIT 1985 |
|
|
1057 |
is equal to a) b) c) d)
is equal to a) b) c) d)
|
IIT 2016 |
|
|
1058 |
(One or more correct answers)
For any two events in the sample space a) 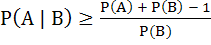 is always true is always true b) 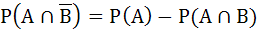 does not hold does not hold c) 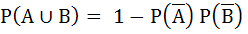 if A and B are independent if A and B are independent d) 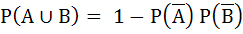 if A and B are disjoint if A and B are disjoint
(One or more correct answers)
For any two events in the sample space a) 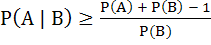 is always true is always true b) 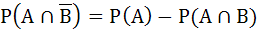 does not hold does not hold c) 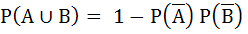 if A and B are independent if A and B are independent d) 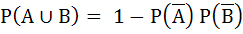 if A and B are disjoint if A and B are disjoint
|
IIT 1991 |
|
|
1059 |
Match the following
Let the function defined in column 1 have domain 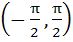 and range (−∞ ∞) and range (−∞ ∞)
| Column1 | Column2 | | i) 1+2x | A) Onto but not one – one | | ii) tanx | B) One to one but not onto | | | C) One to one and onto | | | D) Neither one to one nor onto |
Match the following
Let the function defined in column 1 have domain 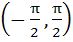 and range (−∞ ∞) and range (−∞ ∞)
| Column1 | Column2 | | i) 1+2x | A) Onto but not one – one | | ii) tanx | B) One to one but not onto | | | C) One to one and onto | | | D) Neither one to one nor onto |
|
IIT 1992 |
|
|
1060 |
Let a, b, c be real numbers such that
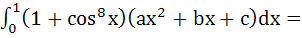 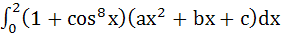
Then ax2 + bx + c = 0 has a) No root in (0, 2) b) At least one root in (0, 2) c) A double root in (0, 2) d) Two imaginary roots
Let a, b, c be real numbers such that
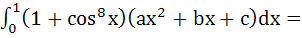 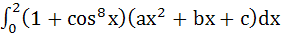
Then ax2 + bx + c = 0 has a) No root in (0, 2) b) At least one root in (0, 2) c) A double root in (0, 2) d) Two imaginary roots
|
IIT 1981 |
|
|
1061 |
The area of the region is a) b) c) d)
The area of the region is a) b) c) d)
|
IIT 2017 |
|
|
1062 |
The total number of local maximum and minimum of the function 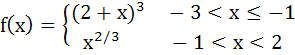
is a) 0 b) 1 c) 2 d) 3
The total number of local maximum and minimum of the function 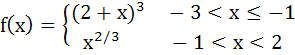
is a) 0 b) 1 c) 2 d) 3
|
IIT 2008 |
|
|
1063 |
The area enclosed by the curve y = sinx + cosx and y = |cosx – sinx| over the interval is a) b) c) d)
The area enclosed by the curve y = sinx + cosx and y = |cosx – sinx| over the interval is a) b) c) d)
|
IIT 2014 |
|
|
1064 |
If 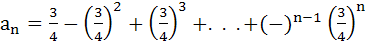 and bn = 1 – an then find the least natural number n0 such that bn > an for all n ≥ n0 and bn = 1 – an then find the least natural number n0 such that bn > an for all n ≥ n0
If 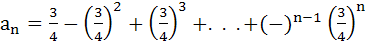 and bn = 1 – an then find the least natural number n0 such that bn > an for all n ≥ n0 and bn = 1 – an then find the least natural number n0 such that bn > an for all n ≥ n0
|
IIT 2006 |
|
|
1065 |
If 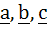 are unit coplanar vectors then the scalar triple product are unit coplanar vectors then the scalar triple product 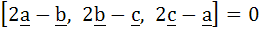 a) 0 b) 1 c) 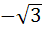 d) 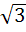
If 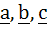 are unit coplanar vectors then the scalar triple product are unit coplanar vectors then the scalar triple product 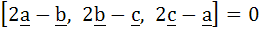 a) 0 b) 1 c) 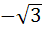 d) 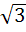
|
IIT 2000 |
|
|
1066 |
One or more than one correct option If the line x = α divides the area of the region R = {(x, y) ∈ ℝ2 : x3 ≤ y ≤ x, 0 ≤ x ≤ 1 into two equal parts then a) b) c) d)
One or more than one correct option If the line x = α divides the area of the region R = {(x, y) ∈ ℝ2 : x3 ≤ y ≤ x, 0 ≤ x ≤ 1 into two equal parts then a) b) c) d)
|
IIT 2017 |
|
|
1067 |
The sides of a triangle inscribed in a given circle subtend angles α, β and γ at the centre. The minimum value of the Arithmetic mean of
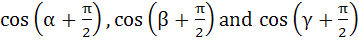
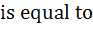
The sides of a triangle inscribed in a given circle subtend angles α, β and γ at the centre. The minimum value of the Arithmetic mean of
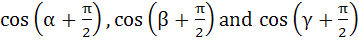
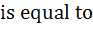
|
IIT 1987 |
|
|
1068 |
The value of a) b) c) d)
The value of a) b) c) d)
|
IIT 2016 |
|
|
1069 |
Let y(x) be the solution of the differential equation . Given that y = 1 when x = 1, then y(e) is equal to a) e b) 0 c) 2 d) 2e
Let y(x) be the solution of the differential equation . Given that y = 1 when x = 1, then y(e) is equal to a) e b) 0 c) 2 d) 2e
|
IIT 2015 |
|
|
1070 |
If Cr stands for 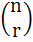 then the sum of the series then the sum of the series
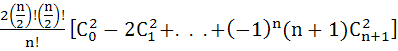
where n is a positive integer, is equal to a) 0 b) (−)n/2(n + 1) c) (−)n/2 (n + 2) d) None of these
If Cr stands for 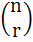 then the sum of the series then the sum of the series
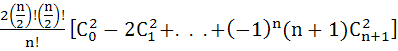
where n is a positive integer, is equal to a) 0 b) (−)n/2(n + 1) c) (−)n/2 (n + 2) d) None of these
|
IIT 1986 |
|
|
1071 |
Let T > 0 be a fixed real number. Suppose f is a continuous function such that for all x 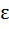 ℝ, f(x + T) = f(x). If ℝ, f(x + T) = f(x). If 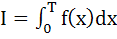 then the value of then the value of 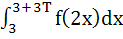 is is a) 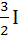 b) 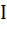 c) 3I d) 6I
Let T > 0 be a fixed real number. Suppose f is a continuous function such that for all x 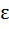 ℝ, f(x + T) = f(x). If ℝ, f(x + T) = f(x). If 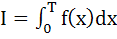 then the value of then the value of 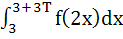 is is a) 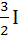 b) 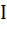 c) 3I d) 6I
|
IIT 2002 |
|
|
1072 |
One or more than one correct options If y(x) satisfies the differential equation y′ − ytanx = 2xsecx and y(0) = 0, then a) b) c) d)
One or more than one correct options If y(x) satisfies the differential equation y′ − ytanx = 2xsecx and y(0) = 0, then a) b) c) d)
|
IIT 2012 |
|
|
1073 |
The sum 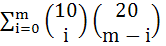 if p > q is maximum when m is if p > q is maximum when m is a) 5 b) 10 c) 15 d) 20
The sum 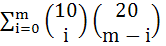 if p > q is maximum when m is if p > q is maximum when m is a) 5 b) 10 c) 15 d) 20
|
IIT 2002 |
|
|
1074 |
At present a firm is manufacturing 2000 items. It is estimated that the rate of change of production P with respect to additional number of workers x is given by . If the firm employs 25 more workers then the new level of production of items is a) 2500 b) 3000 c) 3500 d) 4500
At present a firm is manufacturing 2000 items. It is estimated that the rate of change of production P with respect to additional number of workers x is given by . If the firm employs 25 more workers then the new level of production of items is a) 2500 b) 3000 c) 3500 d) 4500
|
IIT 2013 |
|
|
1075 |
If a, b, c; u, v, w are complex numbers representing the vertices of two triangles such that c = (1 − r)a + rb, w = (1 − r)u + rv where r is a complex number. The two triangles a) have the same area b) are similar c) are congruent d) none of these
If a, b, c; u, v, w are complex numbers representing the vertices of two triangles such that c = (1 − r)a + rb, w = (1 − r)u + rv where r is a complex number. The two triangles a) have the same area b) are similar c) are congruent d) none of these
|
IIT 1985 |
|