|
1026 |
Let An be the area bounded by the curve y = (tanx)n and the line
x = 0, y = 0 and 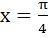 . Prove that for . Prove that for 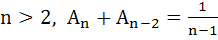 . Hence deduce that . Hence deduce that
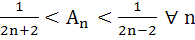
|
IIT 1996 |
|
|
1027 |
Consider the circle x2 + y2 = 9 and the parabola y2 = 8x. They intersect P and Q in the first and fourth quadrants respectively. Tangents to the circle at P and Q intersect the X–axis at R and tangents to the parabola at P and Q intersect the X- axis at S. The radius of the incircle of △PQR is a) 4 b) 3 c)  d) 2
Consider the circle x2 + y2 = 9 and the parabola y2 = 8x. They intersect P and Q in the first and fourth quadrants respectively. Tangents to the circle at P and Q intersect the X–axis at R and tangents to the parabola at P and Q intersect the X- axis at S. The radius of the incircle of △PQR is a) 4 b) 3 c)  d) 2
|
IIT 2007 |
|
|
1028 |
ABCD is a rhombus. The diagonals AC and BD intersect at the point M and satisfy BD = 2AC. If the points D and M represent the complex numbers 1 + i and (2 – i) respectively then find the complex number x + iy represented by A. a) 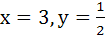 b) 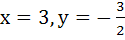 c) 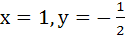 d) 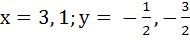
ABCD is a rhombus. The diagonals AC and BD intersect at the point M and satisfy BD = 2AC. If the points D and M represent the complex numbers 1 + i and (2 – i) respectively then find the complex number x + iy represented by A. a) 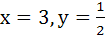 b) 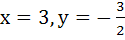 c) 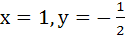 d) 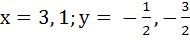
|
IIT 1993 |
|
|
1029 |
Find all possible values of b > 0, so that the area of the bounded region enclosed between the parabolas 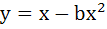 and and 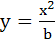 is maximum. is maximum. a) b = 1 b) b ≥ 1 c) b ≤ 1 d) 0 < b < 1
Find all possible values of b > 0, so that the area of the bounded region enclosed between the parabolas 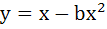 and and 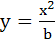 is maximum. is maximum. a) b = 1 b) b ≥ 1 c) b ≤ 1 d) 0 < b < 1
|
IIT 1997 |
|
|
1030 |
Let f(x) = sinx and g(x) = ln|x|. If the ranges of the composition function fog and gof are R1 and R2 respectively then a) 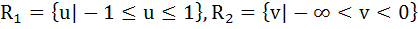 b) 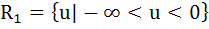 , , 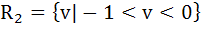 c) 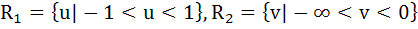 d) 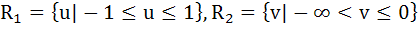
Let f(x) = sinx and g(x) = ln|x|. If the ranges of the composition function fog and gof are R1 and R2 respectively then a) 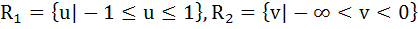 b) 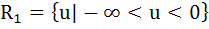 , , 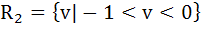 c) 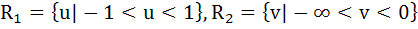 d) 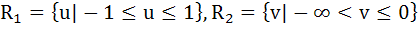
|
IIT 1994 |
|
|
1031 |
Let C1 and C2 be the graph of the function y = x2 and y = 2x respectively. Let C3 be the graph of the function
y = f (x), 0 ≤ x ≤ 1, f (0) = 0. Consider a point P on C1. Let the lines through P, parallel to the axes meet C2 and C3 at Q and R respectively (see figure). If for every position of P (on C1) the area of the shaded regions OPQ and OPR are equal, determine the function f(x). 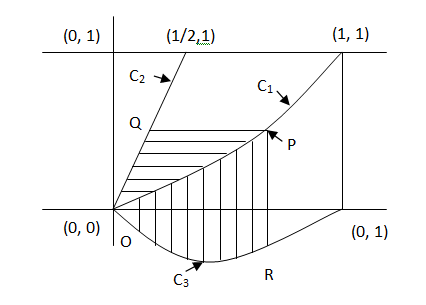
a) x2 – 1 b) x3 – 1 c) x3 – x2 d) 1 + x2 + x3
Let C1 and C2 be the graph of the function y = x2 and y = 2x respectively. Let C3 be the graph of the function
y = f (x), 0 ≤ x ≤ 1, f (0) = 0. Consider a point P on C1. Let the lines through P, parallel to the axes meet C2 and C3 at Q and R respectively (see figure). If for every position of P (on C1) the area of the shaded regions OPQ and OPR are equal, determine the function f(x). 
a) x2 – 1 b) x3 – 1 c) x3 – x2 d) 1 + x2 + x3
|
IIT 1998 |
|
|
1032 |
A hemispherical tank of radius 2 meters is initially full of water and has an outlet of 12cm2 cross section area at the bottom. The outlet is opened at some instant. The flow through the outlet is according to the law 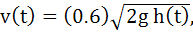 where g(t) and h(t) are respectively the velocity of the flow through the outlet and the height of the water level above the outlet at the time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank. (Hint: Form a differential equation by relating the decrease of water level to the outflow). where g(t) and h(t) are respectively the velocity of the flow through the outlet and the height of the water level above the outlet at the time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank. (Hint: Form a differential equation by relating the decrease of water level to the outflow). a) 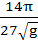 b) 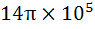 c) 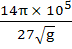 d) 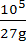
A hemispherical tank of radius 2 meters is initially full of water and has an outlet of 12cm2 cross section area at the bottom. The outlet is opened at some instant. The flow through the outlet is according to the law 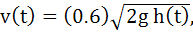 where g(t) and h(t) are respectively the velocity of the flow through the outlet and the height of the water level above the outlet at the time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank. (Hint: Form a differential equation by relating the decrease of water level to the outflow). where g(t) and h(t) are respectively the velocity of the flow through the outlet and the height of the water level above the outlet at the time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank. (Hint: Form a differential equation by relating the decrease of water level to the outflow). a) 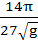 b) 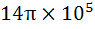 c) 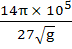 d) 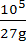
|
IIT 2001 |
|
|
1033 |
Let P be a point on the ellipse 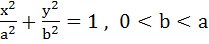 . Let the line parallel to Y–axis passing through P meets the circle . Let the line parallel to Y–axis passing through P meets the circle 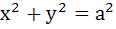 at the point Q such that P and Q are on the same side of the X–axis. For two positive real numbers r and s find the locus of the point R on PQ such that PˆR : RˆQ = r : s and P varies over the ellipse. at the point Q such that P and Q are on the same side of the X–axis. For two positive real numbers r and s find the locus of the point R on PQ such that PˆR : RˆQ = r : s and P varies over the ellipse.
Let P be a point on the ellipse 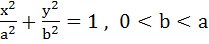 . Let the line parallel to Y–axis passing through P meets the circle . Let the line parallel to Y–axis passing through P meets the circle 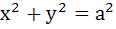 at the point Q such that P and Q are on the same side of the X–axis. For two positive real numbers r and s find the locus of the point R on PQ such that PˆR : RˆQ = r : s and P varies over the ellipse. at the point Q such that P and Q are on the same side of the X–axis. For two positive real numbers r and s find the locus of the point R on PQ such that PˆR : RˆQ = r : s and P varies over the ellipse.
|
IIT 2001 |
|
|
1034 |
Find the area bounded by the curves
x2 = y, x2 = − y and y2 = 4x – 3 a) 1 b) 3 c) 1/3 d) 1/9
Find the area bounded by the curves
x2 = y, x2 = − y and y2 = 4x – 3 a) 1 b) 3 c) 1/3 d) 1/9
|
IIT 2005 |
|
|
1035 |
Let E = {1, 2, 3, 4} and F = {1, 2}, then the number of onto functions from E to F is a) 14 b) 16 c) 12 d) 8
Let E = {1, 2, 3, 4} and F = {1, 2}, then the number of onto functions from E to F is a) 14 b) 16 c) 12 d) 8
|
IIT 2001 |
|
|
1036 |
For a twice differentiable function f(x), g(x) is defined as 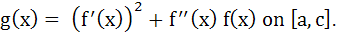 If for a < b < c < d < e, f(a) = 0, f(b) = 2, f(c) = − 1, f(d) = 2, f(e) = 0 then find the maximum number of zeros of g(x). If for a < b < c < d < e, f(a) = 0, f(b) = 2, f(c) = − 1, f(d) = 2, f(e) = 0 then find the maximum number of zeros of g(x). a) 1 b) 2 c) 3 d) 6
For a twice differentiable function f(x), g(x) is defined as 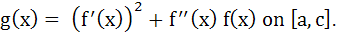 If for a < b < c < d < e, f(a) = 0, f(b) = 2, f(c) = − 1, f(d) = 2, f(e) = 0 then find the maximum number of zeros of g(x). If for a < b < c < d < e, f(a) = 0, f(b) = 2, f(c) = − 1, f(d) = 2, f(e) = 0 then find the maximum number of zeros of g(x). a) 1 b) 2 c) 3 d) 6
|
IIT 2006 |
|
|
1037 |
Find the equation of the normal to the curve 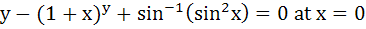
Find the equation of the normal to the curve 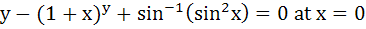
|
IIT 1993 |
|
|
1038 |
The larger of cos (lnθ) and ln (cosθ) if 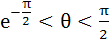 is is a) cos(lnθ) b) ln(cosθ)
The larger of cos (lnθ) and ln (cosθ) if 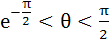 is is a) cos(lnθ) b) ln(cosθ)
|
IIT 1983 |
|
|
1039 |
For any real t, 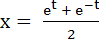 , , 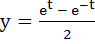 is a point on the hyperbola x2 – y2 = 1. Find the area bounded by the hyperbola and the line joining the centre to the points corresponding to t1 and –t1. is a point on the hyperbola x2 – y2 = 1. Find the area bounded by the hyperbola and the line joining the centre to the points corresponding to t1 and –t1.
For any real t, 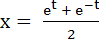 , , 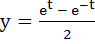 is a point on the hyperbola x2 – y2 = 1. Find the area bounded by the hyperbola and the line joining the centre to the points corresponding to t1 and –t1. is a point on the hyperbola x2 – y2 = 1. Find the area bounded by the hyperbola and the line joining the centre to the points corresponding to t1 and –t1.
|
IIT 1982 |
|
|
1040 |
The integral is equal to a) b) c) d)
The integral is equal to a) b) c) d)
|
IIT 2014 |
|
|
1041 |
X and Y are two sets and f : X → Y. If 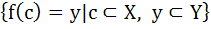 then the true statement is then the true statement is a) 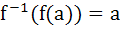 b) 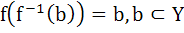 c) 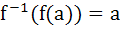 , , 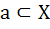 d) 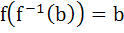
X and Y are two sets and f : X → Y. If 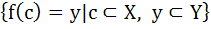 then the true statement is then the true statement is a) 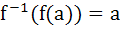 b) 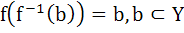 c) 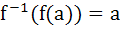 , , 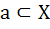 d) 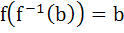
|
IIT 2005 |
|
|
1042 |
Let a and b are non-zero real numbers. Then the equation
(ax2 + by2 + c) (x2 – 5xy + 6y2) = 0 represents a) Four straight lines when c = 0 and a, b are of the same sign b) Two straight lines and a circle when a = b and c is of sign opposite to that of a. c) Two straight lines and a hyperbola when a and b are of the same sign d) A circle and an ellipse when a and b are of the same sign and c is of sign opposite to that of a.
Let a and b are non-zero real numbers. Then the equation
(ax2 + by2 + c) (x2 – 5xy + 6y2) = 0 represents a) Four straight lines when c = 0 and a, b are of the same sign b) Two straight lines and a circle when a = b and c is of sign opposite to that of a. c) Two straight lines and a hyperbola when a and b are of the same sign d) A circle and an ellipse when a and b are of the same sign and c is of sign opposite to that of a.
|
IIT 2008 |
|
|
1043 |
Statement 1: The value of the integral is equal toStatement 2: a) Statement 1 is correct, statement 2 is correct. Statement 2 is correct explanation of statement 1 b) Statement 1 is correct, statement 2 is correct. Statement 2 is not a correct explanation of statement 1 c) Statement 1 is correct, statement 2 is false d) Statement 1 is incorrect, statement 2 is correct
Statement 1: The value of the integral is equal toStatement 2: a) Statement 1 is correct, statement 2 is correct. Statement 2 is correct explanation of statement 1 b) Statement 1 is correct, statement 2 is correct. Statement 2 is not a correct explanation of statement 1 c) Statement 1 is correct, statement 2 is false d) Statement 1 is incorrect, statement 2 is correct
|
IIT 2013 |
|
|
1044 |
Multiple choices
If f(x) = 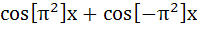 where [x] stands for the greatest integer function then where [x] stands for the greatest integer function then a) 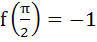 b) 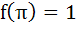 c) 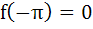 d) 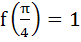
Multiple choices
If f(x) = 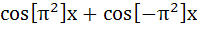 where [x] stands for the greatest integer function then where [x] stands for the greatest integer function then a) 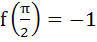 b) 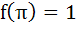 c) 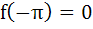 d) 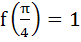
|
IIT 1991 |
|
|
1045 |
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The point of contacts of C with its sides PQ, QR and RP are D, E, F respectively. The line PQ is given by 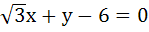 and the point D is and the point D is 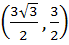 . Further, it is given that the origin and the centre of C are on the same side of the line PQ. Points E and F are given by . Further, it is given that the origin and the centre of C are on the same side of the line PQ. Points E and F are given by a) 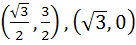 b) 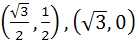 c) 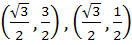 d) 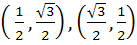
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The point of contacts of C with its sides PQ, QR and RP are D, E, F respectively. The line PQ is given by 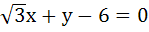 and the point D is and the point D is 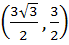 . Further, it is given that the origin and the centre of C are on the same side of the line PQ. Points E and F are given by . Further, it is given that the origin and the centre of C are on the same side of the line PQ. Points E and F are given by a) 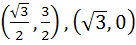 b) 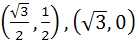 c) 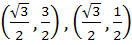 d) 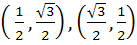
|
IIT 2008 |
|
|
1046 |
One or more than one correct options If then a) b) c) d)
One or more than one correct options If then a) b) c) d)
|
IIT 2017 |
|
|
1047 |
ConsiderL1: 2x + 3y + p – 3 = 0; L2: 2x + 3y + p + 3 = 0 where p is a real number and C : x2 + y2 + 6x – 10y + 30 = 0 Statement 1 – If the line L1 is a chord of the circle C then L2 is not always a diameter of C. Statement 2 - If the line L1 is a diameter of the circle C then L2 is not a chord of the circle.
Which of the following four statements is true? a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true
ConsiderL1: 2x + 3y + p – 3 = 0; L2: 2x + 3y + p + 3 = 0 where p is a real number and C : x2 + y2 + 6x – 10y + 30 = 0 Statement 1 – If the line L1 is a chord of the circle C then L2 is not always a diameter of C. Statement 2 - If the line L1 is a diameter of the circle C then L2 is not a chord of the circle.
Which of the following four statements is true? a) Statement 1 and 2 are true. Statement 2 is a correct explanation for statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation for statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true
|
IIT 2008 |
|
|
1048 |
One or more than one correct options If then a) b) c) d)
One or more than one correct options If then a) b) c) d)
|
IIT 2009 |
|
|
1049 |
If E and F are events with P (E) ≤ P (F) and P (E ∩ F) > 0 then a) occurrence of E ⇒ occurrence of F b) occurrence of F ⇒ occurrence of E c) non-occurrence of E ⇒ non-occurrence of F d) none of the above occurrences hold
If E and F are events with P (E) ≤ P (F) and P (E ∩ F) > 0 then a) occurrence of E ⇒ occurrence of F b) occurrence of F ⇒ occurrence of E c) non-occurrence of E ⇒ non-occurrence of F d) none of the above occurrences hold
|
IIT 1998 |
|
|
1050 |
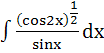 = = 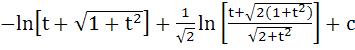
where t2 = cot2x – 1 a) True b) False
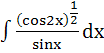 = = 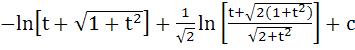
where t2 = cot2x – 1 a) True b) False
|
IIT 1987 |
|