|
1001 |
One or more than one correct option Consider the family of circles whose centre lies on the straight line y = x. If the family of circles is represented by the differential equation Py′′ + Qy′ + 1 = 0 where P, Q are functions of x, y and y′ , then which of the following statements is/are true? a) P = y + x b) P = y – x c) P + Q = 1 – x + y + y′ + (y′)2 d) P − Q = x + y − y′ − (y′)2
One or more than one correct option Consider the family of circles whose centre lies on the straight line y = x. If the family of circles is represented by the differential equation Py′′ + Qy′ + 1 = 0 where P, Q are functions of x, y and y′ , then which of the following statements is/are true? a) P = y + x b) P = y – x c) P + Q = 1 – x + y + y′ + (y′)2 d) P − Q = x + y − y′ − (y′)2
|
IIT 2015 |
|
|
1002 |
Find 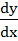 at x = at x = 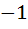 , when , when 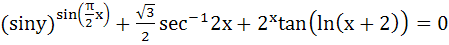
a) 0 b) 1 c) – 1 d) 2
Find 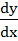 at x = at x = 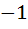 , when , when 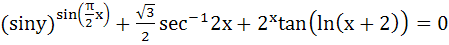
a) 0 b) 1 c) – 1 d) 2
|
IIT 1991 |
|
|
1003 |
One or more than one correct options Let f : (0, ∞) → ℝ be a differentiable function such that for all x ∈ (0, ∞) and f(1) ≠ 1. Then a) b) c) d)
One or more than one correct options Let f : (0, ∞) → ℝ be a differentiable function such that for all x ∈ (0, ∞) and f(1) ≠ 1. Then a) b) c) d)
|
IIT 2016 |
|
|
1004 |
If 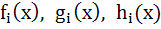 , i = 1, 2, 3 are polynomials in x such that , i = 1, 2, 3 are polynomials in x such that 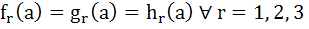 and and F(x) = 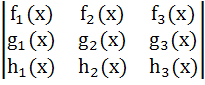
then 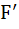 (x) at x = a is equal to (x) at x = a is equal to a) – 1 b) 0 c) 1 d) 2
If 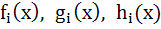 , i = 1, 2, 3 are polynomials in x such that , i = 1, 2, 3 are polynomials in x such that 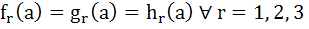 and and F(x) = 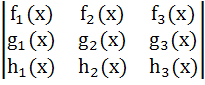
then 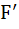 (x) at x = a is equal to (x) at x = a is equal to a) – 1 b) 0 c) 1 d) 2
|
IIT 1985 |
|
|
1005 |
If 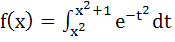 then f (x) increases in then f (x) increases in a) (−2, 2) b) No value of x c) (0, ∞) d) (−∞, 0)
If 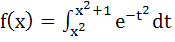 then f (x) increases in then f (x) increases in a) (−2, 2) b) No value of x c) (0, ∞) d) (−∞, 0)
|
IIT 2003 |
|
|
1006 |
A curve passes through the point . Let the slope of the curve at each point (x, y) is , x > 0. Then the equation of the curve is a) b) c) d)
A curve passes through the point . Let the slope of the curve at each point (x, y) is , x > 0. Then the equation of the curve is a) b) c) d)
|
IIT 2013 |
|
|
1007 |
The points 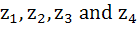 in the complex plane are the vertices of a parallelogram if and only if in the complex plane are the vertices of a parallelogram if and only if a) 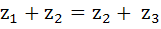 b) 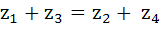 c) 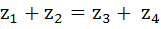 d) None of these
The points 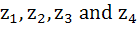 in the complex plane are the vertices of a parallelogram if and only if in the complex plane are the vertices of a parallelogram if and only if a) 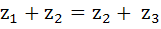 b) 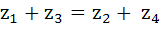 c) 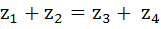 d) None of these
|
IIT 1983 |
|
|
1008 |
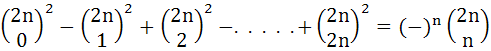
|
IIT 1978 |
|
|
1009 |
Let f:[0, 1] → ℝ (the set all real numbers)be a function. Suppose the function is twice differentiable, f(0) = f(1) = 0 and satisfiesf′′(x) – 2f′(x) + f(x) ≥ ex, x ∈ [0, 1]Which of the following is true? a) b) c) d)
Let f:[0, 1] → ℝ (the set all real numbers)be a function. Suppose the function is twice differentiable, f(0) = f(1) = 0 and satisfiesf′′(x) – 2f′(x) + f(x) ≥ ex, x ∈ [0, 1]Which of the following is true? a) b) c) d)
|
IIT 2013 |
|
|
1010 |
If ω(≠1) is a cube root of unity and 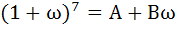 then A and B are respectively then A and B are respectively a) 0, 1 b) 1, 1 c) 1, 0 d) – 1, 1
If ω(≠1) is a cube root of unity and 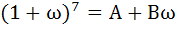 then A and B are respectively then A and B are respectively a) 0, 1 b) 1, 1 c) 1, 0 d) – 1, 1
|
IIT 1995 |
|
|
1011 |
If (1 + x)n = C0 + C1x + C2x2 + . . . + Cnxn, then show that the sum of the products of the Cj’s is taken two at a time represented by
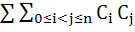 is equal to is equal to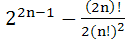
If (1 + x)n = C0 + C1x + C2x2 + . . . + Cnxn, then show that the sum of the products of the Cj’s is taken two at a time represented by
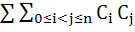 is equal to is equal to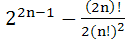
|
IIT 1983 |
|
|
1012 |
Let a, b, c and d be non-zero real numbers. If the point of intersection of lines 4ax + 2ay + c = 0 and 5bx + 2by + d = 0 lie in the fourth quadrants and is equidistant from the two axes, then a) 2bc – 3ad = 0 b) 2bc + 3ad = 0 c) 2ad – 3bc = 0 d) 3bc + 2ad = 0
Let a, b, c and d be non-zero real numbers. If the point of intersection of lines 4ax + 2ay + c = 0 and 5bx + 2by + d = 0 lie in the fourth quadrants and is equidistant from the two axes, then a) 2bc – 3ad = 0 b) 2bc + 3ad = 0 c) 2ad – 3bc = 0 d) 3bc + 2ad = 0
|
IIT 2014 |
|
|
1013 |
One or more than one correct option Let α, λ, μ ∈ ℝ. Consider the system of linear equations αx + 2y = λ 3x – 2y = μWhich of the following statements is/are correct? a) If α = −3, then the system has infinitely many solutions for all values of λ and μ b) If α ≠ −3, then the system of equations has a unique solution for all values of λ and μ c) If λ + μ = 0, then the system has infinitely many solutions for α = −3 d) If λ + μ ≠ 0, then the system has no solution for α = −3
One or more than one correct option Let α, λ, μ ∈ ℝ. Consider the system of linear equations αx + 2y = λ 3x – 2y = μWhich of the following statements is/are correct? a) If α = −3, then the system has infinitely many solutions for all values of λ and μ b) If α ≠ −3, then the system of equations has a unique solution for all values of λ and μ c) If λ + μ = 0, then the system has infinitely many solutions for α = −3 d) If λ + μ ≠ 0, then the system has no solution for α = −3
|
IIT 2016 |
|
|
1014 |
Let 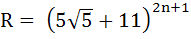 and f = R – [R] where [ ] denotes the greatest integer function. Prove that Rf = 42n + 4 and f = R – [R] where [ ] denotes the greatest integer function. Prove that Rf = 42n + 4
Let 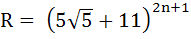 and f = R – [R] where [ ] denotes the greatest integer function. Prove that Rf = 42n + 4 and f = R – [R] where [ ] denotes the greatest integer function. Prove that Rf = 42n + 4
|
IIT 1988 |
|
|
1015 |
One or more than one correct option Circle(s) touching X – axis at a distance 3 from the origin and having an intercept of length on Y – axis is/are a) x2 + y2 – 6x + 8y + 9 = 0 b) x2 + y2 – 6x + 7y + 9 = 0 c) x2 + y2 – 6x − 8y + 9 = 0 d) x2 + y2 – 6x − 7y + 9 = 0
One or more than one correct option Circle(s) touching X – axis at a distance 3 from the origin and having an intercept of length on Y – axis is/are a) x2 + y2 – 6x + 8y + 9 = 0 b) x2 + y2 – 6x + 7y + 9 = 0 c) x2 + y2 – 6x − 8y + 9 = 0 d) x2 + y2 – 6x − 7y + 9 = 0
|
IIT 2013 |
|
|
1016 |
Using induction or otherwise, prove that for any non-negative integers m, n, r and k
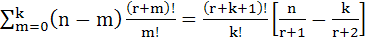
Using induction or otherwise, prove that for any non-negative integers m, n, r and k
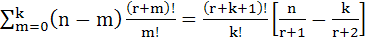
|
IIT 1991 |
|
|
1017 |
Let V be the volume of the parallelepiped formed by the vectors 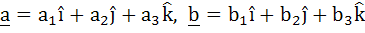 and and 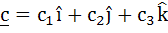 . If ar, br, cr where r = 1, 2, 3 are non-negative real numbers and . If ar, br, cr where r = 1, 2, 3 are non-negative real numbers and 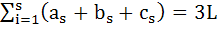 , show that V ≤ L3 , show that V ≤ L3
|
IIT 2002 |
|
|
1018 |
One or more than one correct option A circle S passes through the point (0, 1) and is orthogonal to the circles (x – 1)2 + y2 = 16 and x2 + y2 = 1, then a) Radius of S is 8 b) Radius of S is 7 c) Centre of S is (−7, 1) d) Centre of S is (−8, 1)
One or more than one correct option A circle S passes through the point (0, 1) and is orthogonal to the circles (x – 1)2 + y2 = 16 and x2 + y2 = 1, then a) Radius of S is 8 b) Radius of S is 7 c) Centre of S is (−7, 1) d) Centre of S is (−8, 1)
|
IIT 2014 |
|
|
1019 |
The locus of the midpoint of a chord of the circle 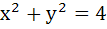 which subtend a right angle at the origin is which subtend a right angle at the origin is a) 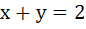 b) 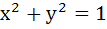 c) 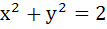 d) 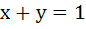
The locus of the midpoint of a chord of the circle 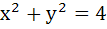 which subtend a right angle at the origin is which subtend a right angle at the origin is a) 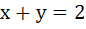 b) 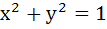 c) 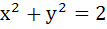 d) 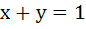
|
IIT 1984 |
|
|
1020 |
If n is a positive integer and 0 ≤ v < π then show that 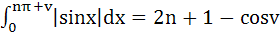
If n is a positive integer and 0 ≤ v < π then show that 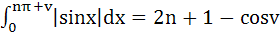
|
IIT 1994 |
|
|
1021 |
A tangent PT is drawn to the circle x2 + y2 = 4 at the point . A straight line L, perpendicular to PT is tangent to the circle (x – 3)2 + y2 = 1A possible equation of L is a) b) c) d)
A tangent PT is drawn to the circle x2 + y2 = 4 at the point . A straight line L, perpendicular to PT is tangent to the circle (x – 3)2 + y2 = 1A possible equation of L is a) b) c) d)
|
IIT 2012 |
|
|
1022 |
Let 0 < Ai < π for i = 1, 2, . . . n. Use mathematical induction to prove that
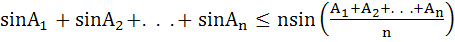
where n ≥ 1 is a natural number.
Let 0 < Ai < π for i = 1, 2, . . . n. Use mathematical induction to prove that
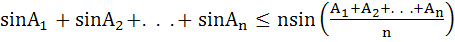
where n ≥ 1 is a natural number.
|
IIT 1997 |
|
|
1023 |
The centre of those circles which touch the circle x2 + y2 – 8x – 8y = 0, externally and also touch the X- axis, lie on a) A circle b) An ellipse which is not a circle c) A hyperbola d) A parabola
The centre of those circles which touch the circle x2 + y2 – 8x – 8y = 0, externally and also touch the X- axis, lie on a) A circle b) An ellipse which is not a circle c) A hyperbola d) A parabola
|
IIT 2016 |
|
|
1024 |
Solve 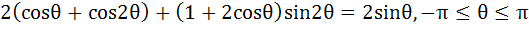
Solve 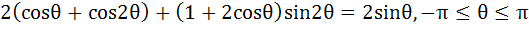
|
IIT 1978 |
|
|
1025 |
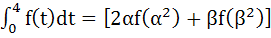 for every 0 < α, β < 2. for every 0 < α, β < 2.
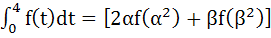 for every 0 < α, β < 2. for every 0 < α, β < 2.
|
IIT 2003 |
|