|
976 |
The value of a) b) c) d)
The value of a) b) c) d)
|
IIT 2016 |
|
|
977 |
Let y(x) be the solution of the differential equation . Given that y = 1 when x = 1, then y(e) is equal to a) e b) 0 c) 2 d) 2e
Let y(x) be the solution of the differential equation . Given that y = 1 when x = 1, then y(e) is equal to a) e b) 0 c) 2 d) 2e
|
IIT 2015 |
|
|
978 |
If Cr stands for 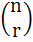 then the sum of the series then the sum of the series
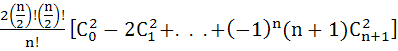
where n is a positive integer, is equal to a) 0 b) (−)n/2(n + 1) c) (−)n/2 (n + 2) d) None of these
If Cr stands for 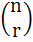 then the sum of the series then the sum of the series
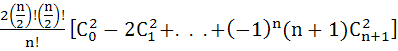
where n is a positive integer, is equal to a) 0 b) (−)n/2(n + 1) c) (−)n/2 (n + 2) d) None of these
|
IIT 1986 |
|
|
979 |
Let T > 0 be a fixed real number. Suppose f is a continuous function such that for all x 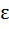 ℝ, f(x + T) = f(x). If ℝ, f(x + T) = f(x). If 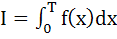 then the value of then the value of 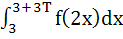 is is a) 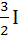 b) 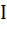 c) 3I d) 6I
Let T > 0 be a fixed real number. Suppose f is a continuous function such that for all x 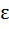 ℝ, f(x + T) = f(x). If ℝ, f(x + T) = f(x). If 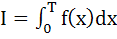 then the value of then the value of 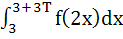 is is a) 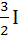 b) 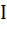 c) 3I d) 6I
|
IIT 2002 |
|
|
980 |
One or more than one correct options If y(x) satisfies the differential equation y′ − ytanx = 2xsecx and y(0) = 0, then a) b) c) d)
One or more than one correct options If y(x) satisfies the differential equation y′ − ytanx = 2xsecx and y(0) = 0, then a) b) c) d)
|
IIT 2012 |
|
|
981 |
The sum 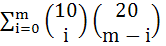 if p > q is maximum when m is if p > q is maximum when m is a) 5 b) 10 c) 15 d) 20
The sum 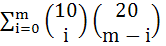 if p > q is maximum when m is if p > q is maximum when m is a) 5 b) 10 c) 15 d) 20
|
IIT 2002 |
|
|
982 |
At present a firm is manufacturing 2000 items. It is estimated that the rate of change of production P with respect to additional number of workers x is given by . If the firm employs 25 more workers then the new level of production of items is a) 2500 b) 3000 c) 3500 d) 4500
At present a firm is manufacturing 2000 items. It is estimated that the rate of change of production P with respect to additional number of workers x is given by . If the firm employs 25 more workers then the new level of production of items is a) 2500 b) 3000 c) 3500 d) 4500
|
IIT 2013 |
|
|
983 |
If a, b, c; u, v, w are complex numbers representing the vertices of two triangles such that c = (1 − r)a + rb, w = (1 − r)u + rv where r is a complex number. The two triangles a) have the same area b) are similar c) are congruent d) none of these
If a, b, c; u, v, w are complex numbers representing the vertices of two triangles such that c = (1 − r)a + rb, w = (1 − r)u + rv where r is a complex number. The two triangles a) have the same area b) are similar c) are congruent d) none of these
|
IIT 1985 |
|
|
984 |
Prove that 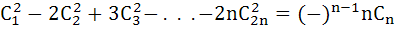
Prove that 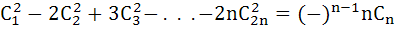
|
IIT 1979 |
|
|
985 |
The question contains Statement – 1(assertion) and Statement – 2 (reason). Let f (x) = 2 + cosx for all real x. Statement 1: For each real t, there exists a point c in [t, t + π] such that 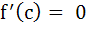 because because Statement 2: f (t) = f[t, t + 2π] for each real t a) Statement 1 and 2 are true. Statement 2 is a correct explanation of Statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation of Statement 1. c) Statement 1 is true and Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
The question contains Statement – 1(assertion) and Statement – 2 (reason). Let f (x) = 2 + cosx for all real x. Statement 1: For each real t, there exists a point c in [t, t + π] such that 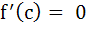 because because Statement 2: f (t) = f[t, t + 2π] for each real t a) Statement 1 and 2 are true. Statement 2 is a correct explanation of Statement 1. b) Statement 1 and 2 are true. Statement 2 is not a correct explanation of Statement 1. c) Statement 1 is true and Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2007 |
|
|
986 |
Let f(x) = (1 – x)2 sin2x + x2 and Which of the following is true? a) g is increasing on (1, ∞) b) g is decreasing on (1, ∞) c) g is increasing on (1, 2) and decreasing on (2, ∞) d) g is decreasing on (1, 2) and increasing on (2, ∞)
Let f(x) = (1 – x)2 sin2x + x2 and Which of the following is true? a) g is increasing on (1, ∞) b) g is decreasing on (1, ∞) c) g is increasing on (1, 2) and decreasing on (2, ∞) d) g is decreasing on (1, 2) and increasing on (2, ∞)
|
IIT 2013 |
|
|
987 |
Use mathematical induction to prove: If n is an odd positive integer
then 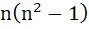 is divisible by 24. is divisible by 24.
Use mathematical induction to prove: If n is an odd positive integer
then 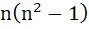 is divisible by 24. is divisible by 24.
|
IIT 1983 |
|
|
988 |
Let PS is the median of the triangle with vertices P(2, 2), Q(6, −1) and R(7, 3), then the equation of the line passing through (1, −1) and parallel to PS is a) 4x – 7y – 11 = 0 b) 2x + 9y + 7 = 0 c) 4x + 7y + 3 = 0 d) 2x – 9y – 11 = 0
Let PS is the median of the triangle with vertices P(2, 2), Q(6, −1) and R(7, 3), then the equation of the line passing through (1, −1) and parallel to PS is a) 4x – 7y – 11 = 0 b) 2x + 9y + 7 = 0 c) 4x + 7y + 3 = 0 d) 2x – 9y – 11 = 0
|
IIT 2014 |
|
|
989 |
One or more than one correct option For a > b > c > 0, the distance between (1, 1) and the point of intersection of the lines ax + by + c = 0 and bx + ay + c = 0 is less than , then a) a + b – c > 0 b) a − b + c < 0 c) a − b + c > 0 d) a + b – c < 0
One or more than one correct option For a > b > c > 0, the distance between (1, 1) and the point of intersection of the lines ax + by + c = 0 and bx + ay + c = 0 is less than , then a) a + b – c > 0 b) a − b + c < 0 c) a − b + c > 0 d) a + b – c < 0
|
IIT 2014 |
|
|
990 |
Using mathematical induction, prove that
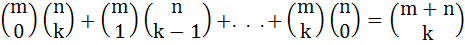
m, n, k are positive integers and 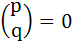 for p < q for p < q
Using mathematical induction, prove that
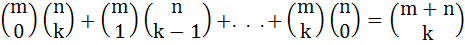
m, n, k are positive integers and 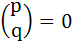 for p < q for p < q
|
IIT 1989 |
|
|
991 |
If one of the diameters of the circle, given by the equation x2 + y2 – 4x + 6y – 12 = 0 is a chord of a circle S whose centre is at (−3, 2), then the radius of S is a) b) c) d)
If one of the diameters of the circle, given by the equation x2 + y2 – 4x + 6y – 12 = 0 is a chord of a circle S whose centre is at (−3, 2), then the radius of S is a) b) c) d)
|
IIT 2016 |
|
|
992 |
If 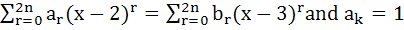 for all k ≥ n then show that for all k ≥ n then show that 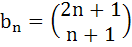
If 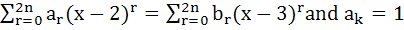 for all k ≥ n then show that for all k ≥ n then show that 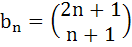
|
IIT 1992 |
|
|
993 |
The function 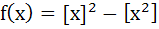 (where [y] is the greatest integer less than or equal to y) is discontinuous at (where [y] is the greatest integer less than or equal to y) is discontinuous at a) All integers b) All integers except 0 and 1 c) All integers except 0 d) All integers except 1
The function 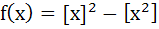 (where [y] is the greatest integer less than or equal to y) is discontinuous at (where [y] is the greatest integer less than or equal to y) is discontinuous at a) All integers b) All integers except 0 and 1 c) All integers except 0 d) All integers except 1
|
IIT 1999 |
|
|
994 |
If 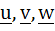 are three non-coplanar unit vectors and α, β, γ are the angles between are three non-coplanar unit vectors and α, β, γ are the angles between 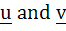 , v and w, w and u respectively and x, y and z are unit vectors along the bisector of the angles α, β, γ respectively. Prove that , v and w, w and u respectively and x, y and z are unit vectors along the bisector of the angles α, β, γ respectively. Prove that
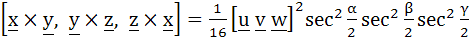
|
IIT 2003 |
|
|
995 |
For how many values of p, the circlex2 + y2 + 2x + 4y – p = 0 and the coordinate axis have exactly three common points a) 0 b) 1 c) 2 d) 3
For how many values of p, the circlex2 + y2 + 2x + 4y – p = 0 and the coordinate axis have exactly three common points a) 0 b) 1 c) 2 d) 3
|
IIT 2014 |
|
|
996 |
A tangent PT is drawn to the circle x2 + y2 = 4 at the point . A straight line L, perpendicular to PT is tangent to the circle (x – 3)2 + y2 = 1A common tangent to the circles is a) x = 4 b) y = 2 c) d)
A tangent PT is drawn to the circle x2 + y2 = 4 at the point . A straight line L, perpendicular to PT is tangent to the circle (x – 3)2 + y2 = 1A common tangent to the circles is a) x = 4 b) y = 2 c) d)
|
IIT 2012 |
|
|
997 |
The integer n, for which 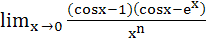 is a finite is a finite non–zero number is a) 1 b) 2 c) 3 d) 4
The integer n, for which 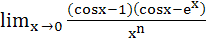 is a finite is a finite non–zero number is a) 1 b) 2 c) 3 d) 4
|
IIT 2002 |
|
|
998 |
The locus of the middle points of the chord of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is a) 20(x2 + y2) – 36x + 45y = 0 b) 20(x2 + y2) + 36x − 45y = 0 c) 36(x2 + y2) – 20x + 45y = 0 d) 36(x2 + y2) + 20x − 45y = 0
The locus of the middle points of the chord of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is a) 20(x2 + y2) – 36x + 45y = 0 b) 20(x2 + y2) + 36x − 45y = 0 c) 36(x2 + y2) – 20x + 45y = 0 d) 36(x2 + y2) + 20x − 45y = 0
|
IIT 2012 |
|
|
999 |
Let 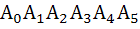 be a regular hexagon in a circle of unit radius. Then the product of the length of the segments be a regular hexagon in a circle of unit radius. Then the product of the length of the segments 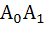 , , 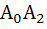 and and 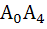 is is a)  b) 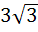 c) 3 d) 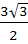
Let 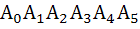 be a regular hexagon in a circle of unit radius. Then the product of the length of the segments be a regular hexagon in a circle of unit radius. Then the product of the length of the segments 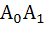 , , 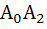 and and 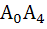 is is a)  b) 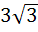 c) 3 d) 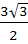
|
IIT 1998 |
|
|
1000 |
f(x) is twice differentiable polynomial function such that f (1) = 1, f (2) = 4, f (3) = 9, then a) there exists at least one x 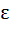 (1, 2) such that (1, 2) such that 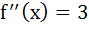 b) there exists at least one x 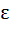 (2, 3) such that (2, 3) such that 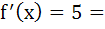 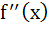 c) 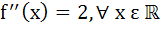 d) there exists at least one x 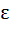 (1, 3) such that (1, 3) such that 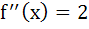
f(x) is twice differentiable polynomial function such that f (1) = 1, f (2) = 4, f (3) = 9, then a) there exists at least one x 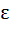 (1, 2) such that (1, 2) such that 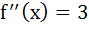 b) there exists at least one x 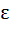 (2, 3) such that (2, 3) such that 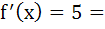 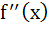 c) 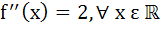 d) there exists at least one x 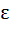 (1, 3) such that (1, 3) such that 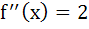
|
IIT 2005 |
|