|
76 |
The numbers are selected from the set S = {1, 2, 3, 4, 5, 6} without replacement one by one. Probability that the minimum of the two numbers is less than 4 is a) 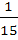 b) 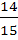 c)  d) 
The numbers are selected from the set S = {1, 2, 3, 4, 5, 6} without replacement one by one. Probability that the minimum of the two numbers is less than 4 is a) 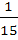 b) 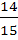 c)  d) 
|
IIT 2003 |
03:06 min
|
|
77 |
Fill in the blank If the product of the roots of the equation
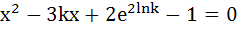 is 7 is 7
Then the roots are real for 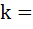 …………. ………….
Fill in the blank If the product of the roots of the equation
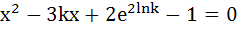 is 7 is 7
Then the roots are real for 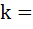 …………. ………….
|
IIT 1984 |
01:40 min
|
|
78 |
Show that the integral
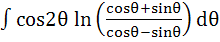 = = 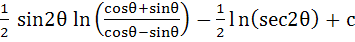
Show that the integral
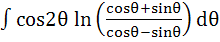 = = 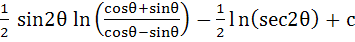
|
IIT 1994 |
06:09 min
|
|
79 |
One Indian and four American men and their wives are to be seated randomly around a circular table. Then the conditional probability that Indian man is seated adjacent to his wife given that each American man is seated adjacent to his wife is a)  b)  c)  d) 
One Indian and four American men and their wives are to be seated randomly around a circular table. Then the conditional probability that Indian man is seated adjacent to his wife given that each American man is seated adjacent to his wife is a)  b)  c)  d) 
|
IIT 2007 |
09:20 min
|
|
80 |
Fill in the blank There are exactly two distinct linear functions ………. and ………. which map {−1, 1} onto {0, 2}.
Fill in the blank There are exactly two distinct linear functions ………. and ………. which map {−1, 1} onto {0, 2}.
|
IIT 1989 |
02:15 min
|
|
81 |
Find three numbers a, b, c between 2 and 18 such that (i) their sum is 25 (ii) 2, a, b are consecutive terms of an Arithmetic Progression and (iii) the numbers b, c, 18 are consecutive terms of a Geometric Progression
Find three numbers a, b, c between 2 and 18 such that (i) their sum is 25 (ii) 2, a, b are consecutive terms of an Arithmetic Progression and (iii) the numbers b, c, 18 are consecutive terms of a Geometric Progression
|
IIT 1983 |
04:09 min
|
|
82 |
Show that 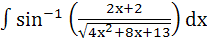 = =
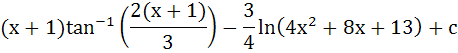
Show that 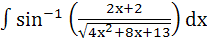 = =
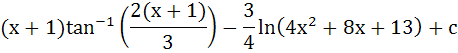
|
IIT 2001 |
06:38 min
|
|
83 |
Let p and q be the position vectors of P and Q respectively with respect to O and 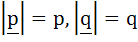 . The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If OR and OS are perpendicular then . The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If OR and OS are perpendicular then a) 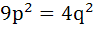 b) 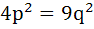 c) 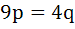 d) 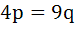
Let p and q be the position vectors of P and Q respectively with respect to O and 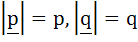 . The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If OR and OS are perpendicular then . The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If OR and OS are perpendicular then a) 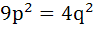 b) 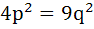 c) 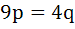 d) 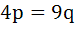
|
IIT 1994 |
02:26 min
|
|
84 |
Let u, v and w be vectors such that 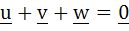 . If . If 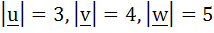 then then 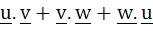 is equal to is equal to a) 47 b) –25 c) 0 d) 25
Let u, v and w be vectors such that 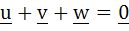 . If . If 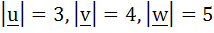 then then 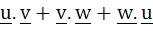 is equal to is equal to a) 47 b) –25 c) 0 d) 25
|
IIT 1995 |
05:00 min
|
|
85 |
(One or more correct answers)
There are four machines and it is known that exactly two of them are faulty. They are tested one by one, in a random order till both the faulty machines are identified. Then the probability that only two tests are needed a)  b)  c)  d) 
(One or more correct answers)
There are four machines and it is known that exactly two of them are faulty. They are tested one by one, in a random order till both the faulty machines are identified. Then the probability that only two tests are needed a)  b)  c)  d) 
|
IIT 1998 |
04:38 min
|
|
86 |
(Subjective problem) Solve 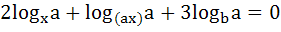
where a > 0, b = a2x.
(Subjective problem) Solve 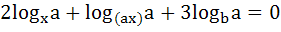
where a > 0, b = a2x.
|
IIT 1978 |
04:27 min
|
|
87 |
Let f : ℝ → ℝ be a differentiable function and f (1) = 4. Then show that the value of 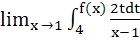 = = 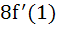
Let f : ℝ → ℝ be a differentiable function and f (1) = 4. Then show that the value of 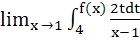 = = 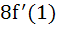
|
IIT 1990 |
02:32 min
|
|
88 |
A box contains 2 black, 4 white and 3 red balls. One ball is drawn at random from the box and kept aside from the remaining balls in the box. Another ball is drawn at random and kept besides the first. This process is repeated till all the balls are drawn from the box. Find the probability that the balls drawn are in the sequence of 2 black, 4 white and 3 red.
A box contains 2 black, 4 white and 3 red balls. One ball is drawn at random from the box and kept aside from the remaining balls in the box. Another ball is drawn at random and kept besides the first. This process is repeated till all the balls are drawn from the box. Find the probability that the balls drawn are in the sequence of 2 black, 4 white and 3 red.
|
IIT 1979 |
03:42 min
|
|
89 |
The expression
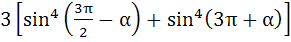
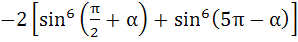 is equal to is equal to a) 0 b) 1 c) 3 d) sin4α + cosα
The expression
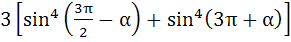
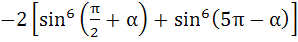 is equal to is equal to a) 0 b) 1 c) 3 d) sin4α + cosα
|
IIT 1986 |
04:12 min
|
|
90 |
If 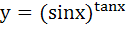 then then 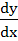 is equal to is equal to a) 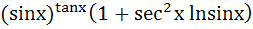 b) 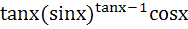 c) 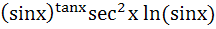 d) 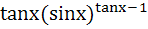
If 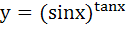 then then 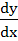 is equal to is equal to a) 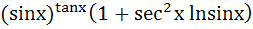 b) 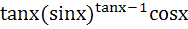 c) 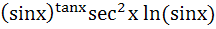 d) 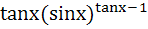
|
IIT 1994 |
01:15 min
|
|
91 |
The value of 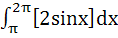 where [.] represents the greatest integer function is where [.] represents the greatest integer function is a) 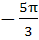 b) 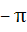 c) 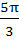 d) 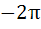
The value of 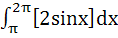 where [.] represents the greatest integer function is where [.] represents the greatest integer function is a) 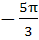 b) 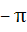 c) 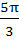 d) 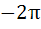
|
IIT 1995 |
07:03 min
|
|
92 |
Let the vectors 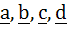 be such that be such that 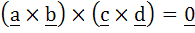 . Let P1 and P2 be the planes determined by the pairs of vectors a, b and c, d respectively. Then the angle between P1 and P2 is . Let P1 and P2 be the planes determined by the pairs of vectors a, b and c, d respectively. Then the angle between P1 and P2 is a) 0 b) 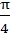 c)  d) 
Let the vectors 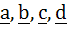 be such that be such that 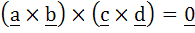 . Let P1 and P2 be the planes determined by the pairs of vectors a, b and c, d respectively. Then the angle between P1 and P2 is . Let P1 and P2 be the planes determined by the pairs of vectors a, b and c, d respectively. Then the angle between P1 and P2 is a) 0 b) 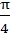 c)  d) 
|
IIT 2000 |
02:05 min
|
|
93 |
If A, B, C be events such that P(A) = 0.3, P(B) = 0.4, P(C) = 0.8, P(AB) = 0.08, P(AC) = 0.28, P(ABC) = 0.09 and P(A ∪ B ∪ C) ≥ 0.75, then show that P(BC) lies in the interval [0.23, 0.48].
If A, B, C be events such that P(A) = 0.3, P(B) = 0.4, P(C) = 0.8, P(AB) = 0.08, P(AC) = 0.28, P(ABC) = 0.09 and P(A ∪ B ∪ C) ≥ 0.75, then show that P(BC) lies in the interval [0.23, 0.48].
|
IIT 1983 |
02:39 min
|
|
94 |
If ω be the cube root of unity then the value of
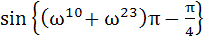 is is a) 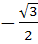 b) 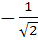 c) 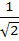 d) 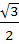
If ω be the cube root of unity then the value of
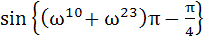 is is a) 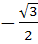 b) 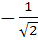 c) 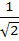 d) 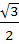
|
IIT 1994 |
02:00 min
|
|
95 |
If 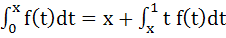 then the value of f(1) is then the value of f(1) is a)  b) 0 c) 1 d) 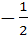
If 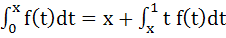 then the value of f(1) is then the value of f(1) is a)  b) 0 c) 1 d) 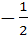
|
IIT 1998 |
01:09 min
|
|
96 |
The value of a so that the volume of parallelopiped formed by 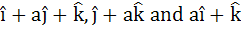 becomes minimum is becomes minimum is a) 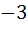 b) 3 c) 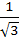 d) 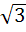
The value of a so that the volume of parallelopiped formed by 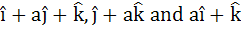 becomes minimum is becomes minimum is a) 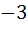 b) 3 c) 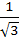 d) 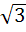
|
IIT 2003 |
02:32 min
|
|
97 |
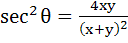 is true if is true if
a) x + y= 0 b) x = y, x ≠ 0 c) x = y d) x ≠ 0, y ≠ 0
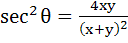 is true if is true if
a) x + y= 0 b) x = y, x ≠ 0 c) x = y d) x ≠ 0, y ≠ 0
|
IIT 1996 |
01:49 min
|
|
98 |
Given 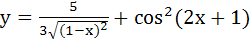 find find 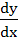
Given 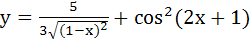 find find 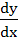
|
IIT 1980 |
03:52 min
|
|
99 |
Let 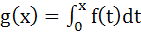 , where f is such that , where f is such that 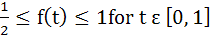 and and 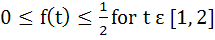 then g(2) satisfies the inequality then g(2) satisfies the inequality a) 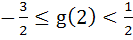 b) 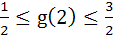 c) 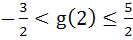 d) 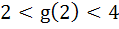
Let 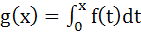 , where f is such that , where f is such that 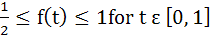 and and 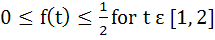 then g(2) satisfies the inequality then g(2) satisfies the inequality a) 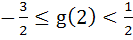 b) 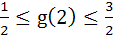 c) 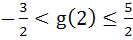 d) 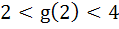
|
IIT 2000 |
02:05 min
|
|
100 |
Suppose the probability for A winning a game against B is 0.4. If A has an option of playing either a best of 3 games or best of 5 games match against B, which option should he choose so that the probability of his winning the match is higher.
Suppose the probability for A winning a game against B is 0.4. If A has an option of playing either a best of 3 games or best of 5 games match against B, which option should he choose so that the probability of his winning the match is higher.
|
IIT 1989 |
05:06 min
|