|
926 |
Let f and g be increasing and decreasing functions, respectively from [0, ∞) to [0, ∞). Let h(x) =f(g(x)). If h(0) = 0 then h(x) – h(t) is a) Always zero b) Always negative c) Always positive d) Strictly increasing e) None of these
Let f and g be increasing and decreasing functions, respectively from [0, ∞) to [0, ∞). Let h(x) =f(g(x)). If h(0) = 0 then h(x) – h(t) is a) Always zero b) Always negative c) Always positive d) Strictly increasing e) None of these
|
IIT 1988 |
|
|
927 |
Let E = {1, 2, 3, 4} and F = {1, 2} then the number of onto functions from E to F is a) 14 b) 16 c) 12 d) 8
Let E = {1, 2, 3, 4} and F = {1, 2} then the number of onto functions from E to F is a) 14 b) 16 c) 12 d) 8
|
IIT 2001 |
|
|
928 |
On the interval [0, 1] the function 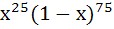 takes the maximum value at the point takes the maximum value at the point a) 0 b)  c)  d) 
On the interval [0, 1] the function 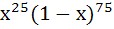 takes the maximum value at the point takes the maximum value at the point a) 0 b)  c)  d) 
|
IIT 1995 |
|
|
929 |
Let f (x) be continuous and g (x) be a discontinuous function. Prove that f (x) + g (x) is a discontinuous function. a) True b) False c) Could be continuous or discontinuous
Let f (x) be continuous and g (x) be a discontinuous function. Prove that f (x) + g (x) is a discontinuous function. a) True b) False c) Could be continuous or discontinuous
|
IIT 1987 |
|
|
930 |
Find the coordinates of the point at which the circles x2 + y2 – 4x – 2y = – 4 and x2 + y2 – 12x – 8y = – 36 touch each other. Also find the equation of the common tangents touching the circles at distinct points.
Find the coordinates of the point at which the circles x2 + y2 – 4x – 2y = – 4 and x2 + y2 – 12x – 8y = – 36 touch each other. Also find the equation of the common tangents touching the circles at distinct points.
|
IIT 1993 |
|
|
931 |
Draw the graph of the function y = [x] + |1 – x|, – 1 ≤ x ≤ 3. Determine the points, if any, where the function is not differentiable. a) y is differentiable everywhere b) y is not differentiable at x = 0 c) y is not differentiable at x = 0, 1, 2 d) y is not differentiable at x = 0, 1, 2 and 3
Draw the graph of the function y = [x] + |1 – x|, – 1 ≤ x ≤ 3. Determine the points, if any, where the function is not differentiable. a) y is differentiable everywhere b) y is not differentiable at x = 0 c) y is not differentiable at x = 0, 1, 2 d) y is not differentiable at x = 0, 1, 2 and 3
|
IIT 1989 |
|
|
932 |
In how many ways can a pack of 52 cards be divided in 4 sets, three of them having 17 cards each and fourth just one card.
In how many ways can a pack of 52 cards be divided in 4 sets, three of them having 17 cards each and fourth just one card.
|
IIT 1979 |
|
|
933 |
The area bounded by the curves 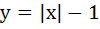 and and 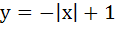 is is
a) 1 b) 2 c) 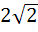 d) 4
The area bounded by the curves 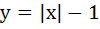 and and 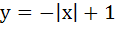 is is
a) 1 b) 2 c) 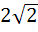 d) 4
|
IIT 2002 |
|
|
934 |
Let ABC be an equilateral triangle inscribed in the circle x2 + y2 = a2. Suppose perpendiculars from A, B, C to the major axis of the ellipse 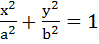 (a > b) meet the ellipse respectively at P, Q, R so that P, Q, R are on the same side of the major axis. Prove that the normals drawn at the points P, Q and R are concurrent. (a > b) meet the ellipse respectively at P, Q, R so that P, Q, R are on the same side of the major axis. Prove that the normals drawn at the points P, Q and R are concurrent.
Let ABC be an equilateral triangle inscribed in the circle x2 + y2 = a2. Suppose perpendiculars from A, B, C to the major axis of the ellipse 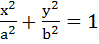 (a > b) meet the ellipse respectively at P, Q, R so that P, Q, R are on the same side of the major axis. Prove that the normals drawn at the points P, Q and R are concurrent. (a > b) meet the ellipse respectively at P, Q, R so that P, Q, R are on the same side of the major axis. Prove that the normals drawn at the points P, Q and R are concurrent.
|
IIT 2000 |
|
|
935 |
Which of the following pieces of data does not uniquely determine an acute angled triangle ABC (R being the radius of the circumcircle). a) a, sinA, sinB b) a, b , c c) a, sinB, R d) a, sinA, R
Which of the following pieces of data does not uniquely determine an acute angled triangle ABC (R being the radius of the circumcircle). a) a, sinA, sinB b) a, b , c c) a, sinB, R d) a, sinA, R
|
IIT 2002 |
|
|
936 |
Let f(x), x ≥ 0 be a non-negative function and let F(x) = 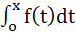 . For some c > 0, f(x) ≤ cF(x) for all x ≥ 0. Then for all x ≥ 0, f(x) = . For some c > 0, f(x) ≤ cF(x) for all x ≥ 0. Then for all x ≥ 0, f(x) = a) 0 b) 1 c) 2 d) 4
Let f(x), x ≥ 0 be a non-negative function and let F(x) = 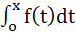 . For some c > 0, f(x) ≤ cF(x) for all x ≥ 0. Then for all x ≥ 0, f(x) = . For some c > 0, f(x) ≤ cF(x) for all x ≥ 0. Then for all x ≥ 0, f(x) = a) 0 b) 1 c) 2 d) 4
|
IIT 2001 |
|
|
937 |
Tangents are drawn from P (6, 8) to the circle 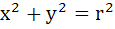 . Find the radius of the circle such that the area of the triangle formed by tangents and chord of contact is maximum. . Find the radius of the circle such that the area of the triangle formed by tangents and chord of contact is maximum.
Tangents are drawn from P (6, 8) to the circle 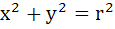 . Find the radius of the circle such that the area of the triangle formed by tangents and chord of contact is maximum. . Find the radius of the circle such that the area of the triangle formed by tangents and chord of contact is maximum.
|
IIT 2003 |
|
|
938 |
Find the natural number a for which
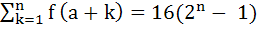
where the function f satisfies the relation f (x + y) = f (x) . f (y)
for all natural numbers x and y and further f (1) = 2 a) 1 b) 2 c) 3 d) 4
Find the natural number a for which
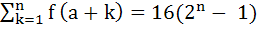
where the function f satisfies the relation f (x + y) = f (x) . f (y)
for all natural numbers x and y and further f (1) = 2 a) 1 b) 2 c) 3 d) 4
|
IIT 1992 |
|
|
939 |
In a certain test 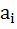 students gave wrong answers to at least i questions where i = 1, 2, …, k. No student gave more than k correct answers. Total number of wrong answers given is . . . students gave wrong answers to at least i questions where i = 1, 2, …, k. No student gave more than k correct answers. Total number of wrong answers given is . . .
In a certain test 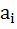 students gave wrong answers to at least i questions where i = 1, 2, …, k. No student gave more than k correct answers. Total number of wrong answers given is . . . students gave wrong answers to at least i questions where i = 1, 2, …, k. No student gave more than k correct answers. Total number of wrong answers given is . . .
|
IIT 1982 |
|
|
940 |
Multiple choice If 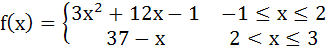 a) f(x) is increasing on [– 1, 2] b) f(x) is continuous on [– 1, 3] c) 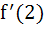 does not exist does not exist d) f(x) has maximum value at x = 2
Multiple choice If 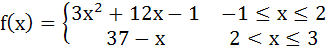 a) f(x) is increasing on [– 1, 2] b) f(x) is continuous on [– 1, 3] c) 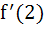 does not exist does not exist d) f(x) has maximum value at x = 2
|
IIT 1993 |
|
|
941 |
If arg(z) < 0 then arg(−z) – arg(z) is equal to a) π b) –π c) – π/2 d) π/2
If arg(z) < 0 then arg(−z) – arg(z) is equal to a) π b) –π c) – π/2 d) π/2
|
IIT 2000 |
|
|
942 |
Multiple choice f(x) is a cubic polynomial with f(2) = 18 and f(1) = − 1. Also f(x) has a local maxima at x = − 1 and 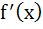 has a local minima at x = 0 then has a local minima at x = 0 then a) The distance between (− 1, 2) and (a, f(a)), where x = a is the point of local minimum, is 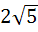 b) f(x) is increasing for 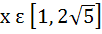 c) f(x) has a local minima at x = 1 d) The value of f(0) = 15
Multiple choice f(x) is a cubic polynomial with f(2) = 18 and f(1) = − 1. Also f(x) has a local maxima at x = − 1 and 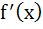 has a local minima at x = 0 then has a local minima at x = 0 then a) The distance between (− 1, 2) and (a, f(a)), where x = a is the point of local minimum, is 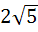 b) f(x) is increasing for 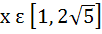 c) f(x) has a local minima at x = 1 d) The value of f(0) = 15
|
IIT 2006 |
|
|
943 |
From the point A (0, 3) on the circle 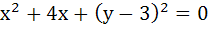 , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . . , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . .
From the point A (0, 3) on the circle 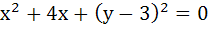 , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . . , a chord AB is drawn and extended to a point M such that AˆM = 2AˆB. The equation of locus of M is . . . . .
|
IIT 1986 |
|
|
944 |
In Δ ABC the median to the side BC is of length 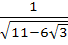 and divides ∠A into 30° and 45°. Then find the length of side BC. and divides ∠A into 30° and 45°. Then find the length of side BC. a) 1 b) 2 c) 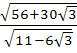 d) 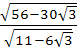
In Δ ABC the median to the side BC is of length 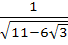 and divides ∠A into 30° and 45°. Then find the length of side BC. and divides ∠A into 30° and 45°. Then find the length of side BC. a) 1 b) 2 c) 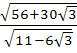 d) 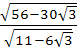
|
IIT 1985 |
|
|
945 |
If f is an even function defined on (−5, 5) then the real values of x satisfying the equation f (x) = 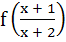 are …………… are …………… a) 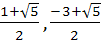 b) 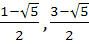 c) 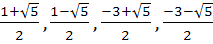 d) 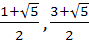
If f is an even function defined on (−5, 5) then the real values of x satisfying the equation f (x) = 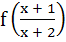 are …………… are …………… a) 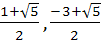 b) 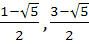 c) 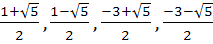 d) 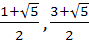
|
IIT 1996 |
|
|
946 |
If ω(≠1) be a cube root of unity and 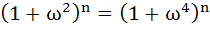 then the least positive value of n is then the least positive value of n is a) 2 b) 3 c) 5 d) 6
If ω(≠1) be a cube root of unity and 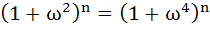 then the least positive value of n is then the least positive value of n is a) 2 b) 3 c) 5 d) 6
|
IIT 2004 |
|
|
947 |
A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in the circle is . . . . .
A circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in the circle is . . . . .
|
IIT 1994 |
|
|
948 |
The number of all possible triplets 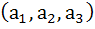 such that such that
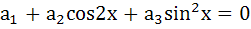 for all x is for all x is a) Zero b) One c) Three d) Infinite e) None
The number of all possible triplets 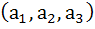 such that such that
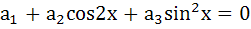 for all x is for all x is a) Zero b) One c) Three d) Infinite e) None
|
IIT 1987 |
|
|
949 |
A swimmer S is in the sea at a distance d km. from the closest point A on a straight shore. The house of the swimmer is on the shore at a distance L km. from A. He can swim at a speed of
u km/hour and walk at a speed of v km/hr (v > u). At what point on the shore should he land so that he reaches his house in the shortest possible time. a) 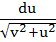 b) 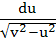 c) 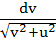 d) 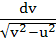
A swimmer S is in the sea at a distance d km. from the closest point A on a straight shore. The house of the swimmer is on the shore at a distance L km. from A. He can swim at a speed of
u km/hour and walk at a speed of v km/hr (v > u). At what point on the shore should he land so that he reaches his house in the shortest possible time. a) 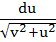 b) 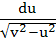 c) 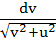 d) 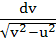
|
IIT 1983 |
|
|
950 |
Sketch the region bounded by the curves
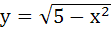 and y = |x – 1| and y = |x – 1|
and find its area. a) 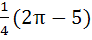 b) 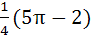 c) 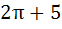 d) 5π + 2
Sketch the region bounded by the curves
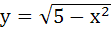 and y = |x – 1| and y = |x – 1|
and find its area. a) 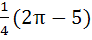 b) 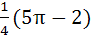 c) 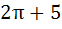 d) 5π + 2
|
IIT 1985 |
|