|
876 |
A ladder rests against a wall at an angle α to the horizontal. If its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal, then 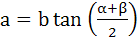 . . a) True b) False
A ladder rests against a wall at an angle α to the horizontal. If its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle β with the horizontal, then 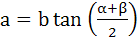 . . a) True b) False
|
IIT 1985 |
|
|
877 |
Let 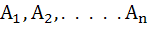 be the vertices of an n sided regular polygon such that be the vertices of an n sided regular polygon such that 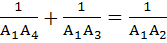 . Then find n. . Then find n. a) 5 b) 6 c) 7 d) 8
Let 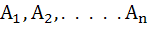 be the vertices of an n sided regular polygon such that be the vertices of an n sided regular polygon such that 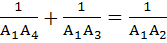 . Then find n. . Then find n. a) 5 b) 6 c) 7 d) 8
|
IIT 1994 |
|
|
878 |
A variable plane at a distance of one unit from the origin cuts the coordinate axes at A, B and C. If the centroid D(x, y, z) of triangle ABC satisfies the relation 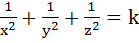 then the value of k is then the value of k is a) 9 b)  c) 1 d) 3
A variable plane at a distance of one unit from the origin cuts the coordinate axes at A, B and C. If the centroid D(x, y, z) of triangle ABC satisfies the relation 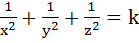 then the value of k is then the value of k is a) 9 b)  c) 1 d) 3
|
IIT 2005 |
|
|
879 |
Find the equation of the plane passing through the points (2, 1, 0), (4, 1, 1), (5, 0, 1). Find the point Q such that its distance from the plane is equal to the point P(2, 1, 6) from the plane and the line joining P and Q is perpendicular to the plane.
Find the equation of the plane passing through the points (2, 1, 0), (4, 1, 1), (5, 0, 1). Find the point Q such that its distance from the plane is equal to the point P(2, 1, 6) from the plane and the line joining P and Q is perpendicular to the plane.
|
IIT 2003 |
|
|
880 |
The unit vector perpendicular to the plane determined by
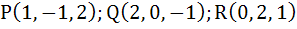 is. is.
The unit vector perpendicular to the plane determined by
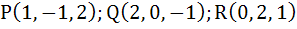 is. is.
|
IIT 1983 |
|
|
881 |
Consider the lines 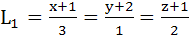 ; ;
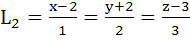
The shortest distance between L1 and L2 is
a) 0 b) 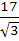 c) 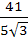 d) 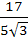
Consider the lines 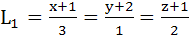 ; ;
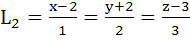
The shortest distance between L1 and L2 is
a) 0 b) 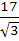 c) 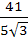 d) 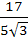
|
IIT 2008 |
|
|
882 |
Let ABCD is the base of parallelopiped T and Aʹ.BʹCʹDʹ be the upper face. The parallelopiped is compressed so that the vertex Aʹ shifts to Aʹʹ on a parallelepiped S. If the volume of the new parallelopiped is 90% of the parallelopiped T, prove that the locus of Aʹʹ is a plane.
Let ABCD is the base of parallelopiped T and Aʹ.BʹCʹDʹ be the upper face. The parallelopiped is compressed so that the vertex Aʹ shifts to Aʹʹ on a parallelepiped S. If the volume of the new parallelopiped is 90% of the parallelopiped T, prove that the locus of Aʹʹ is a plane.
|
IIT 2004 |
|
|
883 |
Show that 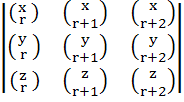 = = 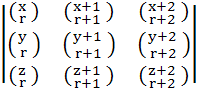
Show that 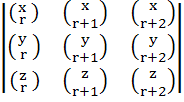 = = 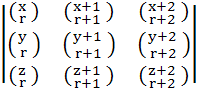
|
IIT 1985 |
|
|
884 |
For all A, B, C, P, Q, R show that
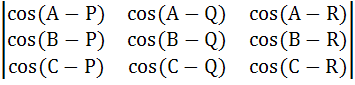 = 0 = 0
For all A, B, C, P, Q, R show that
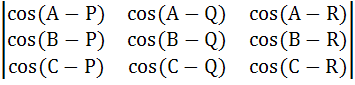 = 0 = 0
|
IIT 1996 |
|
|
885 |
Let f(x) = |x – 1|, then a) 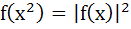 b) 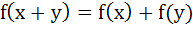 c) 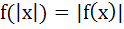 d) None of these
Let f(x) = |x – 1|, then a) 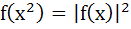 b) 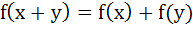 c) 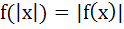 d) None of these
|
IIT 1983 |
|
|
886 |
The differential equation representing the family of curves 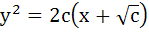 where c is a positive parameter, is of where c is a positive parameter, is of a) Order 1 b) Order 2 c) Degree 3 d) Degree 4
The differential equation representing the family of curves 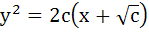 where c is a positive parameter, is of where c is a positive parameter, is of a) Order 1 b) Order 2 c) Degree 3 d) Degree 4
|
IIT 1999 |
|
|
887 |
Let a, b, c be real numbers with a2 + b2 + c2 = 1. Show that the equation represents a straight line
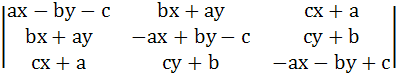 = 0 = 0
Let a, b, c be real numbers with a2 + b2 + c2 = 1. Show that the equation represents a straight line
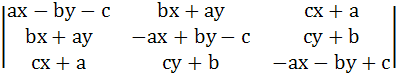 = 0 = 0
|
IIT 2001 |
|
|
888 |
Let 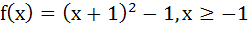 , then the set , then the set 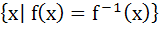 is is a) 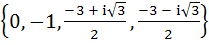 b) 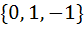 c) 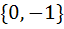 d) ϕ
Let 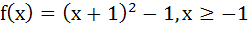 , then the set , then the set 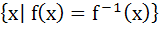 is is a) 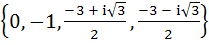 b) 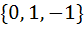 c) 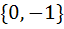 d) ϕ
|
IIT 1995 |
|
|
889 |
A normal is drawn at a point 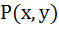 of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is 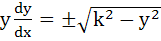
A normal is drawn at a point 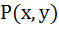 of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is of a curve meeting X-axis at Q. If PQ is of constant length k, then show that the differential equation of the curve is 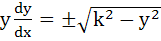
|
IIT 1994 |
|
|
890 |
If f(x) = 3x – 5 then 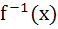 a) is given by 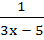 b) is given by 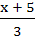 c) does not exist because f is not one-one d) does not exist because f is not onto
If f(x) = 3x – 5 then 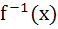 a) is given by 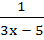 b) is given by 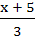 c) does not exist because f is not one-one d) does not exist because f is not onto
|
IIT 1998 |
|
|
891 |
Find the integral solutions of the following system of inequality
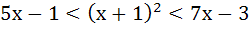 a) x = 1 b) x = 2 c) x = 3 d) x = 4
Find the integral solutions of the following system of inequality
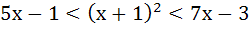 a) x = 1 b) x = 2 c) x = 3 d) x = 4
|
IIT 1979 |
|
|
892 |
Let f(θ) = sinθ (sinθ + sin3θ) then f(θ) a) ≥ 0 only when θ ≥ 0 b) ≤ 0 for all real θ c) ≥ 0 for all real θ d) ≤ θ only when θ ≤ 0
Let f(θ) = sinθ (sinθ + sin3θ) then f(θ) a) ≥ 0 only when θ ≥ 0 b) ≤ 0 for all real θ c) ≥ 0 for all real θ d) ≤ θ only when θ ≤ 0
|
IIT 2000 |
|
|
893 |
Let y = f(x) is a cubic polynomial having maximum at x = − 1 and 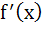 has a minimum at x = 1 and f(−1) = 10, f(1) = − 6. Find the cubic polynomial and also find the distance between the points which are maxima or minima. has a minimum at x = 1 and f(−1) = 10, f(1) = − 6. Find the cubic polynomial and also find the distance between the points which are maxima or minima. a) 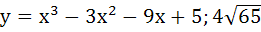 b) 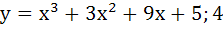 c) 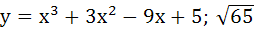 d) 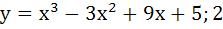
Let y = f(x) is a cubic polynomial having maximum at x = − 1 and 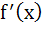 has a minimum at x = 1 and f(−1) = 10, f(1) = − 6. Find the cubic polynomial and also find the distance between the points which are maxima or minima. has a minimum at x = 1 and f(−1) = 10, f(1) = − 6. Find the cubic polynomial and also find the distance between the points which are maxima or minima. a) 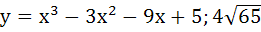 b) 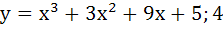 c) 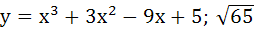 d) 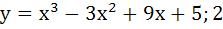
|
IIT 2005 |
|
|
894 |
Each of the following four inequalities given below define a region in the XY–plane. One of these four regions does not have the following property: For any two points (x1, y1) and (x2, y2) in the region, point 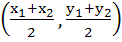 is also in the region. The inequality defining the region that does not have this property is is also in the region. The inequality defining the region that does not have this property is a) x2 + 2y2 ≤ 1 b) max (|x|, |y|) ≤ 1 c) x2 – y2 ≥ 1 d) y2 – x ≤ 0
Each of the following four inequalities given below define a region in the XY–plane. One of these four regions does not have the following property: For any two points (x1, y1) and (x2, y2) in the region, point 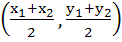 is also in the region. The inequality defining the region that does not have this property is is also in the region. The inequality defining the region that does not have this property is a) x2 + 2y2 ≤ 1 b) max (|x|, |y|) ≤ 1 c) x2 – y2 ≥ 1 d) y2 – x ≤ 0
|
IIT 1981 |
|
|
895 |
The domain of definition of the function 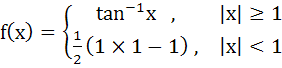 is is a) 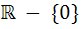 b) 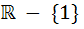 c) 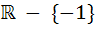 d) 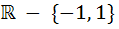
The domain of definition of the function 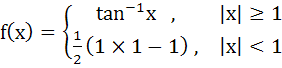 is is a) 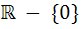 b) 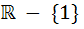 c) 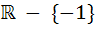 d) 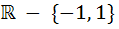
|
IIT 2002 |
|
|
896 |
The set of values of x which ln(1 + x) ≤ x is equal to . . . . a) (−∞, −1) b) (−1, 0) c) (0, 1) d) (1, ∞)
The set of values of x which ln(1 + x) ≤ x is equal to . . . . a) (−∞, −1) b) (−1, 0) c) (0, 1) d) (1, ∞)
|
IIT 1987 |
|
|
897 |
For any positive integers m, n (with n ≥ m), we are given that
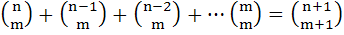
Deduce that
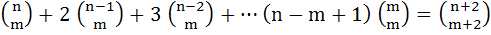
For any positive integers m, n (with n ≥ m), we are given that
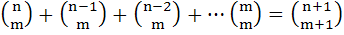
Deduce that
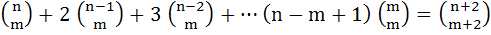
|
IIT 2000 |
|
|
898 |
If A and B are two independent events such that P (A) > 0 and P (B) ≠ 1 then 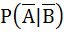 is equal to is equal to a) 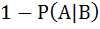 b) 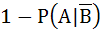 c) 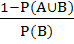 d) 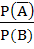
If A and B are two independent events such that P (A) > 0 and P (B) ≠ 1 then 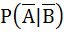 is equal to is equal to a) 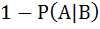 b) 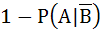 c) 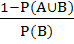 d) 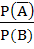
|
IIT 1980 |
|
|
899 |
If , , 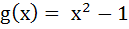 then g(f(x)) is invertible in the domain then g(f(x)) is invertible in the domain a) 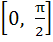 b) 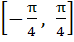 c) 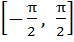 d) 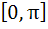
If , , 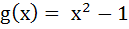 then g(f(x)) is invertible in the domain then g(f(x)) is invertible in the domain a) 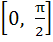 b) 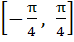 c) 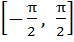 d) 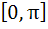
|
IIT 2004 |
|
|
900 |
Evaluate 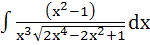 a) 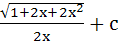 b) 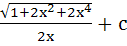 c) 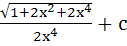 d) 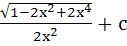
|
IIT 2006 |
|