|
851 |
If a, b, c are distinct positive numbers then the expression
( b + c – a ) ( c + a – b ) ( a + b – c ) –abc is a) Positive b) Negative c) Non–positive d) None of these
If a, b, c are distinct positive numbers then the expression
( b + c – a ) ( c + a – b ) ( a + b – c ) –abc is a) Positive b) Negative c) Non–positive d) None of these
|
IIT 1986 |
|
|
852 |
Let A and B be square matrices of equal degree, then which one is correct amongst the following a) A + B = B + A b) A + B = A – B c) A – B = B – A d) AB = BA
Let A and B be square matrices of equal degree, then which one is correct amongst the following a) A + B = B + A b) A + B = A – B c) A – B = B – A d) AB = BA
|
IIT 1995 |
|
|
853 |
The edges of a parallelepiped are of unit length and are parallel to non-coplanar unit vectors 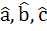 such that such that 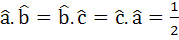 . Then the volume of the parallelepiped is . Then the volume of the parallelepiped is a) 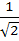 b) 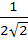 c) 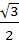 d) 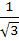
The edges of a parallelepiped are of unit length and are parallel to non-coplanar unit vectors 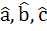 such that such that 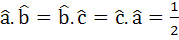 . Then the volume of the parallelepiped is . Then the volume of the parallelepiped is a) 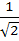 b) 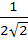 c) 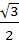 d) 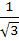
|
IIT 2008 |
|
|
854 |
If P = 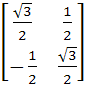 , A = , A = 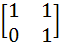 and Q = PAPT and Q = PAPT then PT (Q2005) P is equal to a) 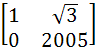 b) 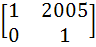 c) 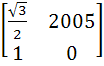 d) 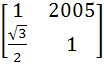
If P = 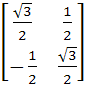 , A = , A = 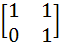 and Q = PAPT and Q = PAPT then PT (Q2005) P is equal to a) 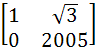 b) 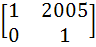 c) 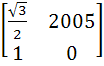 d) 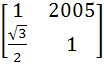
|
IIT 2005 |
|
|
855 |
Consider three planes
P1 : x – y + z = 1 P2 : x + y – z = −1 P3 : x – 3y + 3z = 2 Let L1, L2, L3 be lines of intersection of planes P2 and P3, P3 and P1, and P1 and P2 respectively. Statement 1 – At least two of the lines L1, L2, L3 are non parallel Statement 2 – The three planes do not have a common point. a) Statement 1 is true. Statement 2 is true. Statement 2 is a correct explanation of statement 1. b) Statement 1 is true. Statement 2 is true. Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
Consider three planes
P1 : x – y + z = 1 P2 : x + y – z = −1 P3 : x – 3y + 3z = 2 Let L1, L2, L3 be lines of intersection of planes P2 and P3, P3 and P1, and P1 and P2 respectively. Statement 1 – At least two of the lines L1, L2, L3 are non parallel Statement 2 – The three planes do not have a common point. a) Statement 1 is true. Statement 2 is true. Statement 2 is a correct explanation of statement 1. b) Statement 1 is true. Statement 2 is true. Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2008 |
|
|
856 |
Show that the system of equations
3x – y + 4z = 3
x + 2y − 3z = −2
6x + 5y + λz = −3
has at least one solution for any real number λ ≠ −5. Find the set of solutions if λ = −5 a) 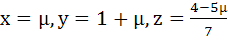 b) 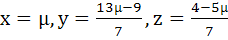 c) 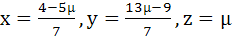 d) 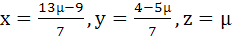
Show that the system of equations
3x – y + 4z = 3
x + 2y − 3z = −2
6x + 5y + λz = −3
has at least one solution for any real number λ ≠ −5. Find the set of solutions if λ = −5 a) 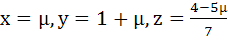 b) 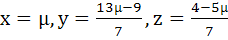 c) 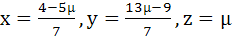 d) 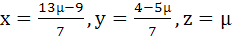
|
IIT 1983 |
|
|
857 |
The solution of primitive equation
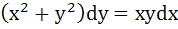 is is 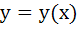 . If . If 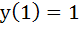 and and 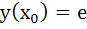 then then 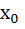 is is a) 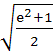 b) 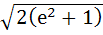 c) 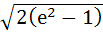 d) 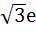
|
IIT 2005 |
|
|
858 |
If 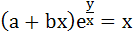 then prove that then prove that 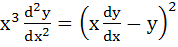
If 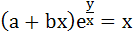 then prove that then prove that 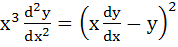
|
IIT 1983 |
|
|
859 |
If M is a 3 x 3 matrix where det (M) = 1 and MMT = I, then prove that det (M – I) = 0.
If M is a 3 x 3 matrix where det (M) = 1 and MMT = I, then prove that det (M – I) = 0.
|
IIT 2004 |
|
|
860 |
Let f(x) be defined for all x > 0 and be continuous. If f(x) satisfies 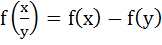 for all x, y and f(e)=1 then for all x, y and f(e)=1 then a) f(x) is bounded b) 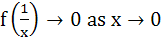 c) x f(x) → 1 as x → 0 d) f(x) = lnx
Let f(x) be defined for all x > 0 and be continuous. If f(x) satisfies 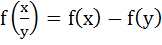 for all x, y and f(e)=1 then for all x, y and f(e)=1 then a) f(x) is bounded b) 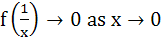 c) x f(x) → 1 as x → 0 d) f(x) = lnx
|
IIT 1995 |
|
|
861 |
The number of values of x where the function 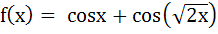 attains its maximum is attains its maximum is a) 0 b) 1 c) 2 d) infinite
The number of values of x where the function 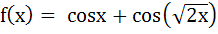 attains its maximum is attains its maximum is a) 0 b) 1 c) 2 d) infinite
|
IIT 1998 |
|
|
862 |
The domain of the definition of the function y given by the equation 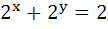 is is a) 0 < x < 1 b) 0 ≤ x ≤ 1 c) 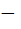 ∞ < x ≤ 0 ∞ < x ≤ 0 d) 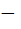 ∞ < x ≤ 1 ∞ < x ≤ 1
The domain of the definition of the function y given by the equation 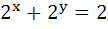 is is a) 0 < x < 1 b) 0 ≤ x ≤ 1 c) 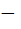 ∞ < x ≤ 0 ∞ < x ≤ 0 d) 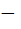 ∞ < x ≤ 1 ∞ < x ≤ 1
|
IIT 2000 |
|
|
863 |
Solution of the differential equation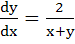 is is
Solution of the differential equation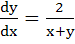 is is
|
IIT 2006 |
|
|
864 |
Let A = 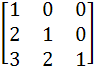 If U1, U2, U3 are column matrices satisfying
AU1 = 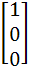 , AU2 = , AU2 = 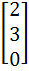 and AU3 = and AU3 = 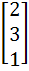 and U is a 3 x 3 matrix whose columns are U1, U2, U3 then the value of [ 3 2 0 ] U 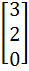 is is a) 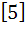 b) 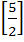 c) 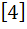 d) 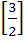
Let A = 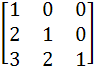 If U1, U2, U3 are column matrices satisfying
AU1 = 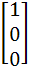 , AU2 = , AU2 = 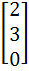 and AU3 = and AU3 = 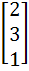 and U is a 3 x 3 matrix whose columns are U1, U2, U3 then the value of [ 3 2 0 ] U 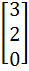 is is a) 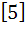 b) 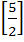 c) 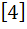 d) 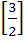
|
IIT 2006 |
|
|
865 |
Let f(x) = 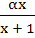 , x ≠ , x ≠ 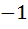 then for what value of α, f(f(x)) = x then for what value of α, f(f(x)) = x a) 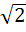 b) 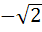 c) 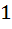 d) 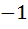
Let f(x) = 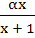 , x ≠ , x ≠ 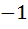 then for what value of α, f(f(x)) = x then for what value of α, f(f(x)) = x a) 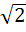 b) 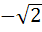 c) 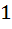 d) 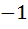
|
IIT 2001 |
|
|
866 |
If 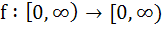 and and 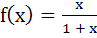 then f is then f is a) One-one and onto b) One-one but not onto c) Onto but not one-one d) Neither one-one nor onto
If 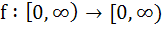 and and 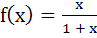 then f is then f is a) One-one and onto b) One-one but not onto c) Onto but not one-one d) Neither one-one nor onto
|
IIT 2003 |
|
|
867 |
If 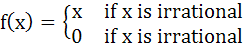
and 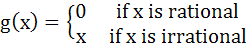
Then f – g is a) Neither one to one nor onto b) One to one and onto c) One to one and into d) Many one and onto
If 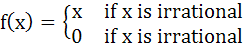
and 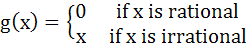
Then f – g is a) Neither one to one nor onto b) One to one and onto c) One to one and into d) Many one and onto
|
IIT 2005 |
|
|
868 |
Let a, b, c, d be real numbers in geometric progression. If u, v, w satisfy the system of equations 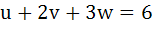
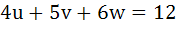
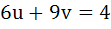
Then show that the roots of the equation
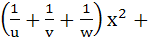
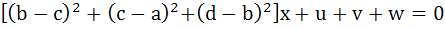
and 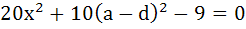 are reciprocal of each other. are reciprocal of each other.
|
IIT 1999 |
|
|
869 |
Subjective Problems
Let f (x + y) = f (x) . f (y) for all x, y. Suppose f (5) = 2 and 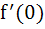 = 3. Find f (5). = 3. Find f (5).
Subjective Problems
Let f (x + y) = f (x) . f (y) for all x, y. Suppose f (5) = 2 and 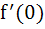 = 3. Find f (5). = 3. Find f (5).
|
IIT 1981 |
|
|
870 |
Find the natural number a for which 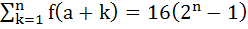 where the function f satisfies the relation f(x + y) = f(x) f(y) for all natural numbers x and y and further f(1) = 2. where the function f satisfies the relation f(x + y) = f(x) f(y) for all natural numbers x and y and further f(1) = 2.
Find the natural number a for which 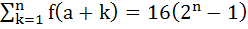 where the function f satisfies the relation f(x + y) = f(x) f(y) for all natural numbers x and y and further f(1) = 2. where the function f satisfies the relation f(x + y) = f(x) f(y) for all natural numbers x and y and further f(1) = 2.
|
IIT 1992 |
|
|
871 |
The interior angles of a polygon are in Arithmetic Progression. The smallest angle is 120° and the common difference is 5. Find the number of sides of the polygon.
The interior angles of a polygon are in Arithmetic Progression. The smallest angle is 120° and the common difference is 5. Find the number of sides of the polygon.
|
IIT 1980 |
|
|
872 |
If 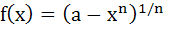 where a > 0 and n is a positive integer then f(f(x)) = x. where a > 0 and n is a positive integer then f(f(x)) = x. a) True b) False
If 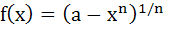 where a > 0 and n is a positive integer then f(f(x)) = x. where a > 0 and n is a positive integer then f(f(x)) = x. a) True b) False
|
IIT 1983 |
|
|
873 |
A vector a has components 2p and 1 with respect to a rectangular cartesian system. This system is rotated through a certain angle about the origin in the counter clockwise sense. If with respect to new system a has components p + 1 and 1 then a) p ≠ 0 b) p = 1 or p = 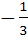 c) p = −1 or 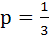 d) p = 1 or p = −1 e) None of these
A vector a has components 2p and 1 with respect to a rectangular cartesian system. This system is rotated through a certain angle about the origin in the counter clockwise sense. If with respect to new system a has components p + 1 and 1 then a) p ≠ 0 b) p = 1 or p = 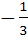 c) p = −1 or 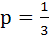 d) p = 1 or p = −1 e) None of these
|
IIT 1986 |
|
|
874 |
The domain of the function 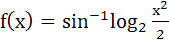 is is
The domain of the function 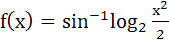 is is
|
IIT 1984 |
|
|
875 |
If f is an even function defined on (−5, 5) then the four real values of x satisfying the equation 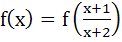 are are
If f is an even function defined on (−5, 5) then the four real values of x satisfying the equation 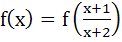 are are
|
IIT 1996 |
|