|
826 |
If α is a repeated root of a quadratic equation f(x) = 0 and A(x), B(x), C(x) be polynomials of degree 3, 4, 5 respectively, Then show that
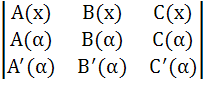 is divisible by f(x) where prime denotes the derivatives.
If α is a repeated root of a quadratic equation f(x) = 0 and A(x), B(x), C(x) be polynomials of degree 3, 4, 5 respectively, Then show that
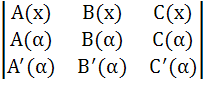 is divisible by f(x) where prime denotes the derivatives.
|
IIT 1984 |
|
|
827 |
The differential equation 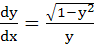 determines a family of circles with determines a family of circles with a) Variable radii and a fixed centre ( 0, 1) b) Variable radii and a fixed centre ( 0, -1) c) Fixed radius and a variable centre along the X-axis d) Fixed radius and a variable centre along the Y-axis
The differential equation 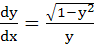 determines a family of circles with determines a family of circles with a) Variable radii and a fixed centre ( 0, 1) b) Variable radii and a fixed centre ( 0, -1) c) Fixed radius and a variable centre along the X-axis d) Fixed radius and a variable centre along the Y-axis
|
IIT 2007 |
|
|
828 |
Prove that for all values of θ
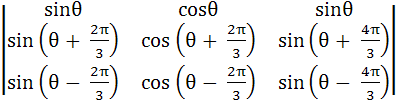 = 0 = 0
Prove that for all values of θ
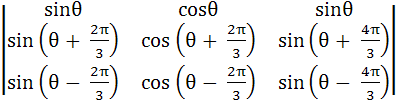 = 0 = 0
|
IIT 2000 |
|
|
829 |
If 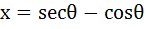 and and 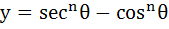 , then show that , then show that
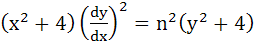
|
IIT 1989 |
|
|
830 |
A = 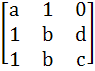 , B = , B = 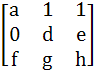 , U = , U = 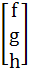 , V = , V = 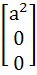 If AX = U has infinitely many solutions, prove that BX = V has no unique solution. Also prove that if afd ≠ 0 then BX = V has no solution. X is a vector.
|
IIT 2004 |
|
|
831 |
If 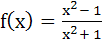 , for every real number x, then the minimum value of f , for every real number x, then the minimum value of f a) does not exist because f is unbounded b) is not attained even though f is bounded c) is equal to 1 d) is equal to –1
If 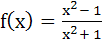 , for every real number x, then the minimum value of f , for every real number x, then the minimum value of f a) does not exist because f is unbounded b) is not attained even though f is bounded c) is equal to 1 d) is equal to –1
|
IIT 1998 |
|
|
832 |
Let u (x) and v (x) satisfy the differential equations 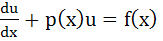 and and 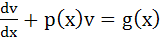 where p (x), f (x) and g (x) are continuous functions. If where p (x), f (x) and g (x) are continuous functions. If  u (x1) > v (x1) for some x1 and f (x) > g (x) for all x > x1, prove that at any point (x, y) where x > x1 does not satisfy the equations y = u (x) and y = v (x) u (x1) > v (x1) for some x1 and f (x) > g (x) for all x > x1, prove that at any point (x, y) where x > x1 does not satisfy the equations y = u (x) and y = v (x)
|
IIT 1997 |
|
|
833 |
The function 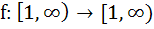 is defined by is defined by 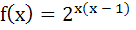 then then 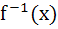 is is a) 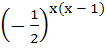 b) 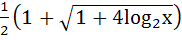 c) 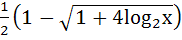 d) None of these
The function 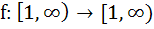 is defined by is defined by 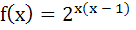 then then 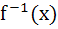 is is a) 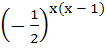 b) 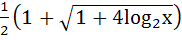 c) 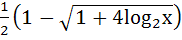 d) None of these
|
IIT 1999 |
|
|
834 |
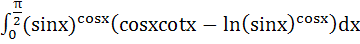 is is
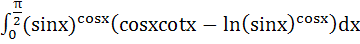 is is
|
IIT 2006 |
|
|
835 |
Suppose 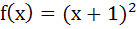 for x ≥ for x ≥ 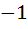 . If g(x) is the function whose graph is the reflection of f(x) with respect to the line y = x then g(x) equals . If g(x) is the function whose graph is the reflection of f(x) with respect to the line y = x then g(x) equals a) 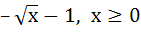 b) 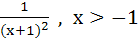 c) 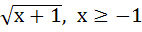 d) 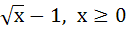
Suppose 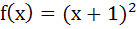 for x ≥ for x ≥ 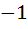 . If g(x) is the function whose graph is the reflection of f(x) with respect to the line y = x then g(x) equals . If g(x) is the function whose graph is the reflection of f(x) with respect to the line y = x then g(x) equals a) 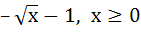 b) 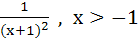 c) 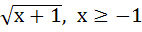 d) 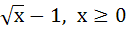
|
IIT 2002 |
|
|
836 |
Domain of definition of the function 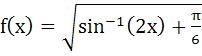 for real values of x is for real values of x is a) 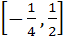 b) 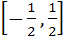 c) 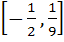 d) 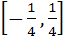
Domain of definition of the function 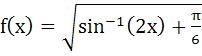 for real values of x is for real values of x is a) 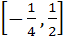 b) 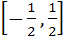 c) 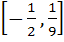 d) 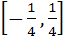
|
IIT 2003 |
|
|
837 |
Let λ and α be real. Find the set of all values of λ for which the system of linear equations
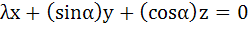
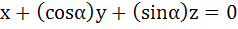
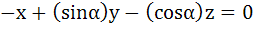
has a non-trivial solution. For λ = 1 find the value of α.
|
IIT 1993 |
|
|
838 |
Let f be a one–one function with domain {x, y, z} and range {1, 2, 3}. It is given that exactly one of the following statements is true and remaining statements are false f (1) = 1, f (y) ≠ 1, f (z) ≠ 2. Determine 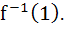
Let f be a one–one function with domain {x, y, z} and range {1, 2, 3}. It is given that exactly one of the following statements is true and remaining statements are false f (1) = 1, f (y) ≠ 1, f (z) ≠ 2. Determine 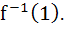
|
IIT 1982 |
|
|
839 |
The value of 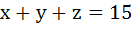 . Given that a, x, y, z, b are in Arithmetic Progression while the value of . Given that a, x, y, z, b are in Arithmetic Progression while the value of 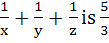 . If a, x, y, z, b are in Harmonic Progression then find a and b. . If a, x, y, z, b are in Harmonic Progression then find a and b.
The value of 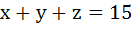 . Given that a, x, y, z, b are in Arithmetic Progression while the value of . Given that a, x, y, z, b are in Arithmetic Progression while the value of 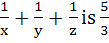 . If a, x, y, z, b are in Harmonic Progression then find a and b. . If a, x, y, z, b are in Harmonic Progression then find a and b.
|
IIT 1978 |
|
|
840 |
Let {x} and [x] denote the fractional and integral part of a real number x respectively. Solve 4{x} = x + [x]
Let {x} and [x] denote the fractional and integral part of a real number x respectively. Solve 4{x} = x + [x]
|
IIT 1994 |
|
|
841 |
If f1(x) and f2(x) are defined by domains D1 and D2 respectively then f1(x) + f2(x) is defined as on D1 ⋂ D2 a) True b) False
If f1(x) and f2(x) are defined by domains D1 and D2 respectively then f1(x) + f2(x) is defined as on D1 ⋂ D2 a) True b) False
|
IIT 1988 |
|
|
842 |
If 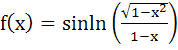 then the domain of f(x) is then the domain of f(x) is
If 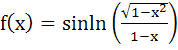 then the domain of f(x) is then the domain of f(x) is
|
IIT 1985 |
|
|
843 |
The real numbers x1, x2, x3 satisfying the equation x3 – x2 + βx + γ = 0 are in Arithmetic Progression. Find the interval in which β and γ lie.
The real numbers x1, x2, x3 satisfying the equation x3 – x2 + βx + γ = 0 are in Arithmetic Progression. Find the interval in which β and γ lie.
|
IIT 1996 |
|
|
844 |
Let p, q, r be three mutually perpendicular vectors of the same magnitude. If x satisfies the equation p 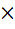 ((x – q) ((x – q) 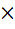 p) + q p) + q 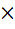 ((x – r) ((x – r) 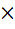 q) + r q) + r 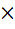 ((x – p) ((x – p) 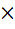 r) = 0 then x is given by r) = 0 then x is given by a) 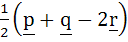 b) 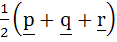 c) 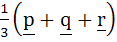 d) 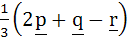
|
IIT 1997 |
|
|
845 |
Let f(x) be a non constant differentiable function defined on (−∞, ∞) such that f(x) = f(1 – x) and 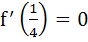 then then a) 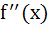 vanishes at twice an (0, 1) vanishes at twice an (0, 1) b) 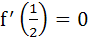 c) 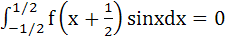 d) 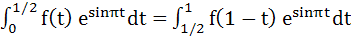
Let f(x) be a non constant differentiable function defined on (−∞, ∞) such that f(x) = f(1 – x) and 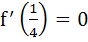 then then a) 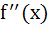 vanishes at twice an (0, 1) vanishes at twice an (0, 1) b) 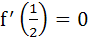 c) 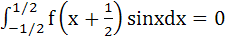 d) 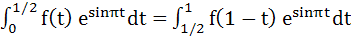
|
IIT 2008 |
|
|
846 |
Let 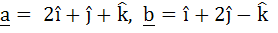 and a unit vector c be coplanar. If c is perpendicular to a then c is equal to and a unit vector c be coplanar. If c is perpendicular to a then c is equal to a) 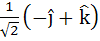 b) 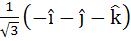 c) 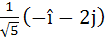 d) 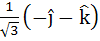
Let 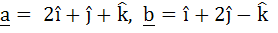 and a unit vector c be coplanar. If c is perpendicular to a then c is equal to and a unit vector c be coplanar. If c is perpendicular to a then c is equal to a) 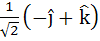 b) 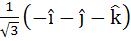 c) 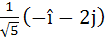 d) 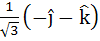
|
IIT 1999 |
|
|
847 |
Number of solutions of 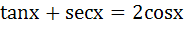 lying in the interval lying in the interval 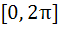 is is a) 0 b) 1 c) 2 d) 3
Number of solutions of 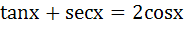 lying in the interval lying in the interval 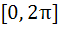 is is a) 0 b) 1 c) 2 d) 3
|
IIT 1993 |
|
|
848 |
If three complex numbers are in Arithmetic Progression, then they lie on a circle in a complex plane. a) True b) False
If three complex numbers are in Arithmetic Progression, then they lie on a circle in a complex plane. a) True b) False
|
IIT 1985 |
|
|
849 |
Multiple choice The vector 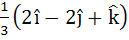 is is a) A unit vector b) Makes an angle  with the vector with the vector 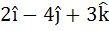 c) Parallel to vector 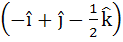 d) Perpendicular to the vector 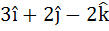
Multiple choice The vector 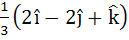 is is a) A unit vector b) Makes an angle  with the vector with the vector 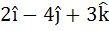 c) Parallel to vector 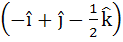 d) Perpendicular to the vector 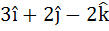
|
IIT 1994 |
|
|
850 |
A1, A2, …… , An are the vertices of a regular polygon with n sides and O is the centre. Show that
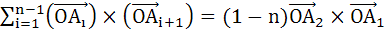
A1, A2, …… , An are the vertices of a regular polygon with n sides and O is the centre. Show that
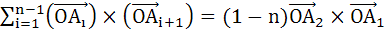
|
IIT 1982 |
|