|
801 |
Multiple choice Let 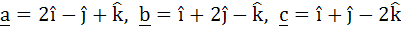 be three vectors. A vector in the plane of b and c whose projection on a is of magnitude be three vectors. A vector in the plane of b and c whose projection on a is of magnitude 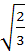 is is a) 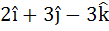 b) 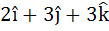 c) 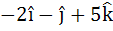 d) 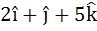
Multiple choice Let 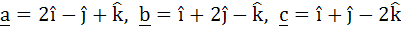 be three vectors. A vector in the plane of b and c whose projection on a is of magnitude be three vectors. A vector in the plane of b and c whose projection on a is of magnitude 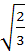 is is a) 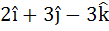 b) 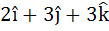 c) 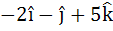 d) 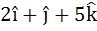
|
IIT 1993 |
|
|
802 |
Let A be vector parallel to the line of intersection of planes P1 and P2. Plane P1 is parallel to the vectors 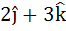 and and 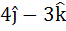 and that P2 is parallel to and that P2 is parallel to 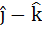 and and 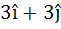 , then the angle between vector A and a given vector , then the angle between vector A and a given vector 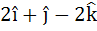 is is a)  b) 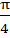 c)  d) 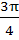
|
IIT 2006 |
|
|
803 |
Find the range of values of t for which 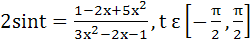 a) (−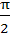 , − , −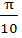 ) ) b) ( 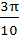 , ,  ) ) c) (− 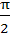 , − , − 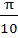 ) U ( ) U ( 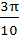 , ,  ) ) d) (−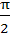 , , 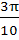 ) )
|
IIT 2005 |
|
|
804 |
A vector A has components A1, A2, A3 in a right handed rectangular cartesian coordinate system OXYZ. The coordinate system is rotated about the X–axis through an angle  . Find the components of A in the new co-ordinate system in terms of A1, A2, A3. . Find the components of A in the new co-ordinate system in terms of A1, A2, A3.
A vector A has components A1, A2, A3 in a right handed rectangular cartesian coordinate system OXYZ. The coordinate system is rotated about the X–axis through an angle  . Find the components of A in the new co-ordinate system in terms of A1, A2, A3. . Find the components of A in the new co-ordinate system in terms of A1, A2, A3.
|
IIT 1983 |
|
|
805 |
The value of 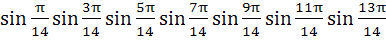 is equal to is equal to a)  b) 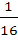 c) 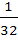 d) 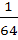
The value of 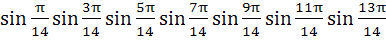 is equal to is equal to a)  b) 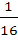 c) 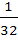 d) 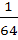
|
IIT 1991 |
|
|
806 |
In a triangle OAB, E is the midpoint of BO and D is a point on AB such that AD : DB = 2 : 1. If OD and AE intercept at P determine the ratio OP : PD using vector methods.
In a triangle OAB, E is the midpoint of BO and D is a point on AB such that AD : DB = 2 : 1. If OD and AE intercept at P determine the ratio OP : PD using vector methods.
|
IIT 1989 |
|
|
807 |
The position vectors of the vertices A, B, C of a tetrahedron are 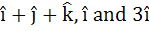 respectively. The altitude from the vertex D to the opposite face ABC meets the median line through A of the triangle ABC at E. If the length of the side AD is 4 and the volume of the tetrahedron is respectively. The altitude from the vertex D to the opposite face ABC meets the median line through A of the triangle ABC at E. If the length of the side AD is 4 and the volume of the tetrahedron is 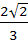 . Find the position vector of E or all possible positions. . Find the position vector of E or all possible positions.
The position vectors of the vertices A, B, C of a tetrahedron are 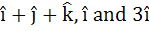 respectively. The altitude from the vertex D to the opposite face ABC meets the median line through A of the triangle ABC at E. If the length of the side AD is 4 and the volume of the tetrahedron is respectively. The altitude from the vertex D to the opposite face ABC meets the median line through A of the triangle ABC at E. If the length of the side AD is 4 and the volume of the tetrahedron is 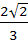 . Find the position vector of E or all possible positions. . Find the position vector of E or all possible positions.
|
IIT 1996 |
|
|
808 |
For any two vectors u and v prove that i) 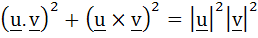 ii) 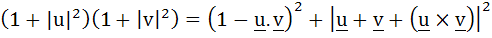
For any two vectors u and v prove that i) 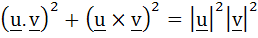 ii) 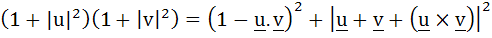
|
IIT 1998 |
|
|
809 |
True/False If 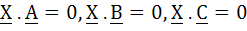 for some non zero vector X then for some non zero vector X then 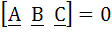 a) True b) False
True/False If 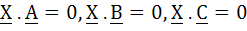 for some non zero vector X then for some non zero vector X then 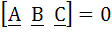 a) True b) False
|
IIT 1983 |
|
|
810 |
If 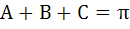 then then 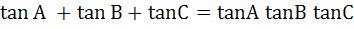 a) True b) False
If 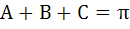 then then 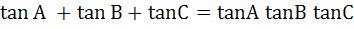 a) True b) False
|
IIT 1979 |
|
|
811 |
Let 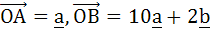 and and 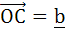 where O, A and B are non-collinear points. Let p denote the area of the quadrilateral OABC and let q denote the area of the quadrilateral with OA and OC as adjacent sides. If p = kq then k = . . . . . where O, A and B are non-collinear points. Let p denote the area of the quadrilateral OABC and let q denote the area of the quadrilateral with OA and OC as adjacent sides. If p = kq then k = . . . . .
Let 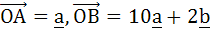 and and 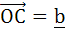 where O, A and B are non-collinear points. Let p denote the area of the quadrilateral OABC and let q denote the area of the quadrilateral with OA and OC as adjacent sides. If p = kq then k = . . . . . where O, A and B are non-collinear points. Let p denote the area of the quadrilateral OABC and let q denote the area of the quadrilateral with OA and OC as adjacent sides. If p = kq then k = . . . . .
|
IIT 1997 |
|
|
812 |
Prove that 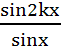 = 2[cosx + cos3x + cos5x + … + cos(2k−1)x] for any positive integer k. Hence prove that = 2[cosx + cos3x + cos5x + … + cos(2k−1)x] for any positive integer k. Hence prove that 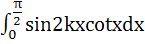 = = 
|
IIT 1990 |
|
|
813 |
The function
f(x) =|px – q| + r |x|, x ε (−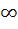 , , 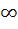 ) )
where p > 0, q > 0, r > 0 assumes minimum value on one point if a) p ≠ q b) r = q c) r ≠ p d) r = p = q
The function
f(x) =|px – q| + r |x|, x ε (−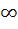 , , 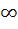 ) )
where p > 0, q > 0, r > 0 assumes minimum value on one point if a) p ≠ q b) r = q c) r ≠ p d) r = p = q
|
IIT 1995 |
|
|
814 |
Let f : R → R be any function defined g : R → R by g (x) = |f (x)| for all x. Then g is a) onto if f is onto b) one to one if f is one to one c) continuous if f is continuous d) differentiable if f is differentiable
Let f : R → R be any function defined g : R → R by g (x) = |f (x)| for all x. Then g is a) onto if f is onto b) one to one if f is one to one c) continuous if f is continuous d) differentiable if f is differentiable
|
IIT 2000 |
|
|
815 |
If f : [ 1, 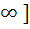 → [ 2, → [ 2, 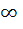 ] is given by f (x) = x + ] is given by f (x) = x +  then then 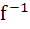 ( x ) is given by ( x ) is given by a) 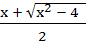 b) 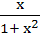 c) 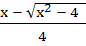 d) 1 + 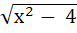
|
IIT 2001 |
|
|
816 |
The function of f : R → R be defined by f (x) = 2x + sinx for x ε R . Then f is a) one-one and onto b) one-one but not onto c) onto but not one-one d) neither one-one nor onto
The function of f : R → R be defined by f (x) = 2x + sinx for x ε R . Then f is a) one-one and onto b) one-one but not onto c) onto but not one-one d) neither one-one nor onto
|
IIT 2002 |
|
|
817 |
Multiple choice There exists a triangle ABC satisfying the conditions a) bsinA = a, A <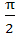 b) bsinA > a, A >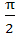 c) bsinA > a, A <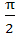 d) bsinA < a, A <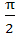 , b > a , b > a e) bsinA < a, A >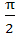 , b = a , b = a
Multiple choice There exists a triangle ABC satisfying the conditions a) bsinA = a, A <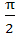 b) bsinA > a, A >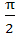 c) bsinA > a, A <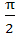 d) bsinA < a, A <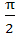 , b > a , b > a e) bsinA < a, A >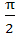 , b = a , b = a
|
IIT 1986 |
|
|
818 |
With usual notation if in a triangle ABC, 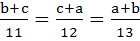 then then 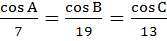 . .
a) True b) False
With usual notation if in a triangle ABC, 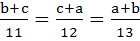 then then 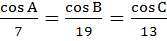 . .
a) True b) False
|
IIT 1984 |
|
|
819 |
If in a triangle ABC, cosA cosB + sinA sinB sin C = 1 then show that a : b : c = 1 : 1 : 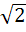 a) True b) False
If in a triangle ABC, cosA cosB + sinA sinB sin C = 1 then show that a : b : c = 1 : 1 : 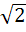 a) True b) False
|
IIT 1986 |
|
|
820 |
If the lines 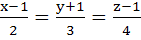 and and 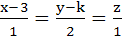 intersect then the value of k is intersect then the value of k is a)  b)  c) 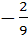 d) 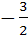
If the lines 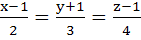 and and 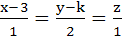 intersect then the value of k is intersect then the value of k is a)  b)  c) 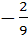 d) 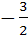
|
IIT 2004 |
|
|
821 |
The area of a triangle whose vertices are
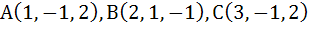 is is
The area of a triangle whose vertices are
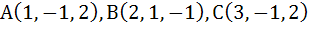 is is
|
IIT 1983 |
|
|
822 |
The parameter on which the value of the determinant
Δ = 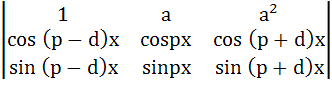
does not depend upon is a) a b) p c) d d) x
The parameter on which the value of the determinant
Δ = 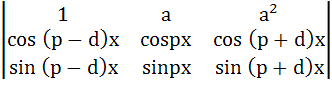
does not depend upon is a) a b) p c) d d) x
|
IIT 1997 |
|
|
823 |
Consider the lines 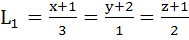 ; ;
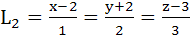
The unit vector perpendicular to both L1 and L2 is
a) 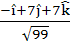 b) 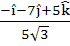 c) 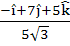 d) 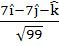
Consider the lines 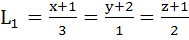 ; ;
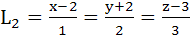
The unit vector perpendicular to both L1 and L2 is
a) 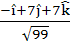 b) 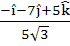 c) 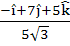 d) 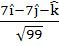
|
IIT 2008 |
|
|
824 |
If b > a then the equation ( x – a ) ( x – b )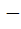 1 = 0 has 1 = 0 has a) Both roots in [ a, b ] b) Both roots in ( 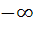 , a ) , a ) c) Both roots in ( 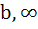 ) ) d) One root in ( 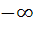 , a ) and other in ( , a ) and other in (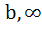 ) )
If b > a then the equation ( x – a ) ( x – b )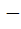 1 = 0 has 1 = 0 has a) Both roots in [ a, b ] b) Both roots in ( 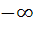 , a ) , a ) c) Both roots in ( 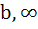 ) ) d) One root in ( 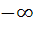 , a ) and other in ( , a ) and other in (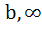 ) )
|
IIT 2000 |
|
|
825 |
For what value of m does the system of equations 3x + my = m, 2x − 5y = 20 have a solution satisfying the condition x > 0, y > 0. a) m 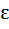 (−∞, ∞) (−∞, ∞) b) m 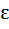 (−∞, −15) ∪ (30, ∞) (−∞, −15) ∪ (30, ∞) c) 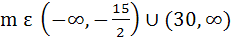 d) 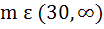
For what value of m does the system of equations 3x + my = m, 2x − 5y = 20 have a solution satisfying the condition x > 0, y > 0. a) m 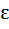 (−∞, ∞) (−∞, ∞) b) m 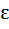 (−∞, −15) ∪ (30, ∞) (−∞, −15) ∪ (30, ∞) c) 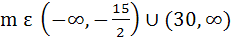 d) 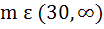
|
IIT 1979 |
|