|
776 |
If 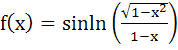 then the domain of f(x) is then the domain of f(x) is
If 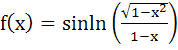 then the domain of f(x) is then the domain of f(x) is
|
IIT 1985 |
|
|
777 |
The real numbers x1, x2, x3 satisfying the equation x3 – x2 + βx + γ = 0 are in Arithmetic Progression. Find the interval in which β and γ lie.
The real numbers x1, x2, x3 satisfying the equation x3 – x2 + βx + γ = 0 are in Arithmetic Progression. Find the interval in which β and γ lie.
|
IIT 1996 |
|
|
778 |
Let p, q, r be three mutually perpendicular vectors of the same magnitude. If x satisfies the equation p 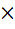 ((x – q) ((x – q) 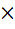 p) + q p) + q 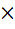 ((x – r) ((x – r) 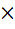 q) + r q) + r 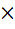 ((x – p) ((x – p) 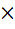 r) = 0 then x is given by r) = 0 then x is given by a) 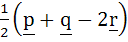 b) 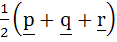 c) 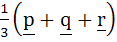 d) 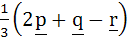
|
IIT 1997 |
|
|
779 |
Let f(x) be a non constant differentiable function defined on (−∞, ∞) such that f(x) = f(1 – x) and 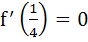 then then a) 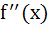 vanishes at twice an (0, 1) vanishes at twice an (0, 1) b) 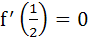 c) 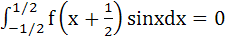 d) 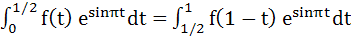
Let f(x) be a non constant differentiable function defined on (−∞, ∞) such that f(x) = f(1 – x) and 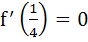 then then a) 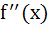 vanishes at twice an (0, 1) vanishes at twice an (0, 1) b) 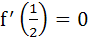 c) 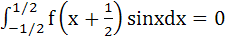 d) 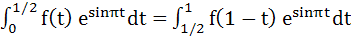
|
IIT 2008 |
|
|
780 |
Let 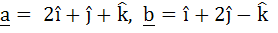 and a unit vector c be coplanar. If c is perpendicular to a then c is equal to and a unit vector c be coplanar. If c is perpendicular to a then c is equal to a) 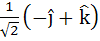 b) 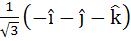 c) 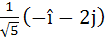 d) 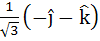
Let 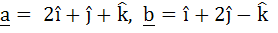 and a unit vector c be coplanar. If c is perpendicular to a then c is equal to and a unit vector c be coplanar. If c is perpendicular to a then c is equal to a) 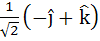 b) 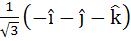 c) 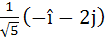 d) 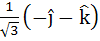
|
IIT 1999 |
|
|
781 |
Number of solutions of 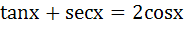 lying in the interval lying in the interval 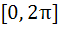 is is a) 0 b) 1 c) 2 d) 3
Number of solutions of 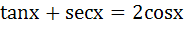 lying in the interval lying in the interval 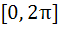 is is a) 0 b) 1 c) 2 d) 3
|
IIT 1993 |
|
|
782 |
If three complex numbers are in Arithmetic Progression, then they lie on a circle in a complex plane. a) True b) False
If three complex numbers are in Arithmetic Progression, then they lie on a circle in a complex plane. a) True b) False
|
IIT 1985 |
|
|
783 |
Multiple choice The vector 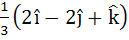 is is a) A unit vector b) Makes an angle  with the vector with the vector 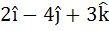 c) Parallel to vector 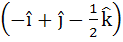 d) Perpendicular to the vector 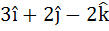
Multiple choice The vector 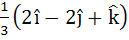 is is a) A unit vector b) Makes an angle  with the vector with the vector 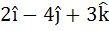 c) Parallel to vector 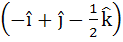 d) Perpendicular to the vector 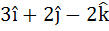
|
IIT 1994 |
|
|
784 |
A1, A2, …… , An are the vertices of a regular polygon with n sides and O is the centre. Show that
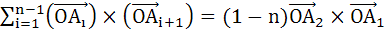
A1, A2, …… , An are the vertices of a regular polygon with n sides and O is the centre. Show that
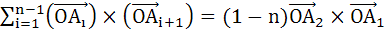
|
IIT 1982 |
|
|
785 |
If A, B, C are such that |B| = |C|. Prove that 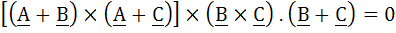
If A, B, C are such that |B| = |C|. Prove that 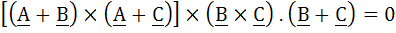
|
IIT 1997 |
|
|
786 |
Let u and v be unit vectors. If w is a vector such that 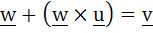 , then prove that , then prove that 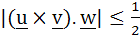 and that equality holds if and only if and that equality holds if and only if 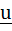 is perpendicular to is perpendicular to 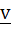
|
IIT 1999 |
|
|
787 |
Let n be an odd integer. If sin nθ = 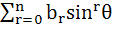 for every value of θ, then for every value of θ, then a) 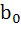 = 1, = 1, 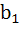 = 3 = 3 b) 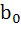 = 0, = 0, 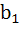 = n = n c) 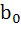 = −1, = −1, 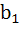 = n = n d) 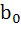 = 1, = 1, 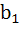 = = 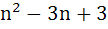
|
IIT 1998 |
|
|
788 |
If 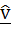 is the unit vector along the incident ray, is the unit vector along the incident ray, 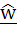 is a unit vector along the reflected ray and is a unit vector along the reflected ray and 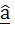 is a unit vector along the outward drawn normal to the plane mirror at the point of incidence. Find is a unit vector along the outward drawn normal to the plane mirror at the point of incidence. Find 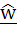 in terms of in terms of 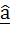 and and 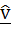
|
IIT 2005 |
|
|
789 |
True / False For any three vectors a, b and c
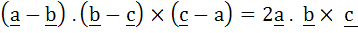 a) True b) False
True / False For any three vectors a, b and c
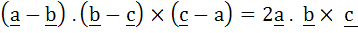 a) True b) False
|
IIT 1989 |
|
|
790 |
Multiple choices
For a positive integer n, let
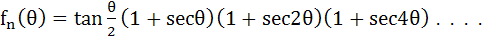
. . .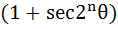 then then a) 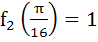 b) 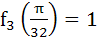 c) 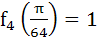 d) 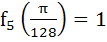
Multiple choices
For a positive integer n, let
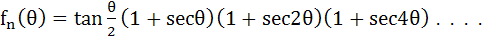
. . .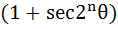 then then a) 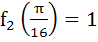 b) 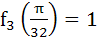 c) 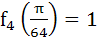 d) 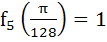
|
IIT 1999 |
|
|
791 |
For all 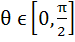 , , 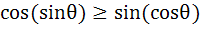 a) True b) False
For all 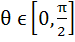 , , 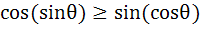 a) True b) False
|
IIT 1981 |
|
|
792 |
Let f (x) = |x – 1| then a) f (x2) = |f (x)|2 b) f (x + y) = f (x) + f (y) c) f (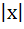 ) = |f (x)| ) = |f (x)| d) None of these
Let f (x) = |x – 1| then a) f (x2) = |f (x)|2 b) f (x + y) = f (x) + f (y) c) f (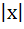 ) = |f (x)| ) = |f (x)| d) None of these
|
IIT 1983 |
|
|
793 |
Let the vectors 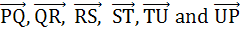 represent the edges of a regular hexagon represent the edges of a regular hexagon Statement 1 - 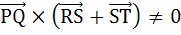 because because Statement 2 - 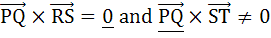 a) Statement 1 and 2 are true and Statement 2 is a correct explanation of statement 1. b) Statement 1 and 2 are true and Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
Let the vectors 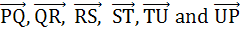 represent the edges of a regular hexagon represent the edges of a regular hexagon Statement 1 - 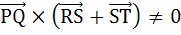 because because Statement 2 - 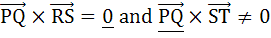 a) Statement 1 and 2 are true and Statement 2 is a correct explanation of statement 1. b) Statement 1 and 2 are true and Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2007 |
|
|
794 |
Find the smallest possible value of p for which the equation
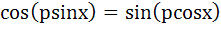 a) 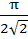 b) 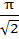 c)  d) 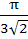
Find the smallest possible value of p for which the equation
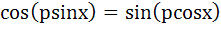 a) 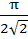 b) 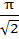 c)  d) 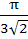
|
IIT 1995 |
|
|
795 |
If f (x) = 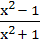 for every real x then the minimum value of f for every real x then the minimum value of f a) does not exist because f is unbounded b) is not attained even though f is bounded c) is equal to 1 d) is equal to −1
If f (x) = 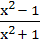 for every real x then the minimum value of f for every real x then the minimum value of f a) does not exist because f is unbounded b) is not attained even though f is bounded c) is equal to 1 d) is equal to −1
|
IIT 1998 |
|
|
796 |
Find the larger of cos(lnθ) and ln(cosθ) if 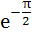 < θ < < θ <  . . a) cos(lnθ) b) ln(cosθ) c) Neither is larger throughout the interval
Find the larger of cos(lnθ) and ln(cosθ) if 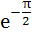 < θ < < θ <  . . a) cos(lnθ) b) ln(cosθ) c) Neither is larger throughout the interval
|
IIT 1983 |
|
|
797 |
If the function f : [ 1, 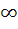 ) → [ 1, ) → [ 1, 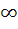 ) is defined by f (x) = 2x(x – 1) then ) is defined by f (x) = 2x(x – 1) then
f -1(x) is a) 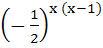 b)  ( (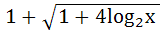 ) ) c)  ( (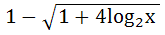 ) ) d) 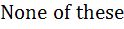
|
IIT 1999 |
|
|
798 |
If 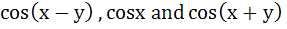 are in harmonic progression then are in harmonic progression then 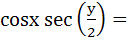 ………… ………… a) 1 b) 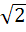 c) 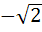 d) 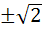
If 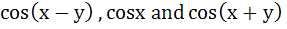 are in harmonic progression then are in harmonic progression then 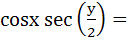 ………… ………… a) 1 b) 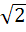 c) 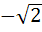 d) 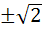
|
IIT 1997 |
|
|
799 |
If 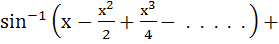 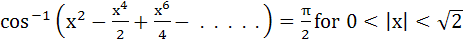
then x equals a)  b) 1 c) 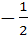 d) –1
If 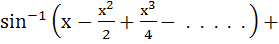 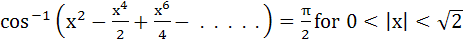
then x equals a)  b) 1 c) 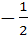 d) –1
|
IIT 1999 |
|
|
800 |
Let f ( x ) = 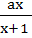 , x ≠ , x ≠ 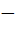 1 then for what value of a is f ( f (x)) = x 1 then for what value of a is f ( f (x)) = x a) 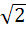 b) 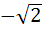 c) 1 d) 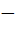 1 1
Let f ( x ) = 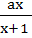 , x ≠ , x ≠ 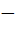 1 then for what value of a is f ( f (x)) = x 1 then for what value of a is f ( f (x)) = x a) 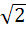 b) 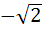 c) 1 d)  1 1
|
IIT 2001 |
|