|
751 |
For any odd integer n ≥ 1,
n3 – (n – 1)3 + . . . + (−)n – 1 13 = . . .
For any odd integer n ≥ 1,
n3 – (n – 1)3 + . . . + (−)n – 1 13 = . . .
|
IIT 1996 |
|
|
752 |
A unit vector which is orthogonal to the vectors 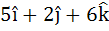 and and coplanar with the vectors 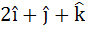 and and 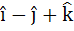 is is a) 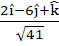 b) 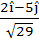 c) 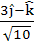 d) 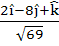
A unit vector which is orthogonal to the vectors 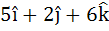 and and coplanar with the vectors 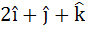 and and 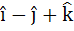 is is a) 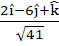 b) 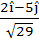 c) 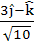 d) 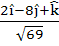
|
IIT 2004 |
|
|
753 |
The area of the equilateral triangle which contains three coins of unit radius is a) 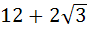 square units square units b) 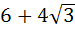 square units square units c) 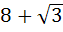 square units square units d) 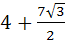 square units square units
The area of the equilateral triangle which contains three coins of unit radius is a) 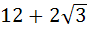 square units square units b) 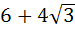 square units square units c) 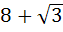 square units square units d) 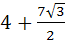 square units square units
|
IIT 2005 |
|
|
754 |
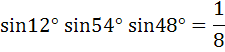
a) True b) False
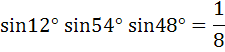
a) True b) False
|
IIT 1982 |
|
|
755 |
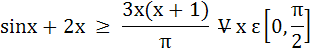
a) True b) False
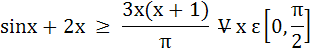
a) True b) False
|
IIT 2004 |
|
|
756 |
Match the following 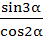 is is | Column 1 | Column 2 | | i) Positive | A) (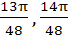 ) ) | | ii) Negative | B) (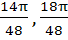 ) ) | | | C) (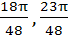 ) ) | | | D) (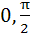 ) ) |
Match the following 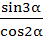 is is | Column 1 | Column 2 | | i) Positive | A) (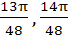 ) ) | | ii) Negative | B) (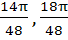 ) ) | | | C) (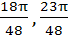 ) ) | | | D) (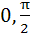 ) ) |
|
IIT 1992 |
|
|
757 |
If the vectors b, c, d, are not coplanar then prove that a is parallel to the vector 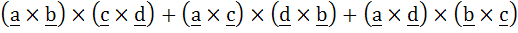
If the vectors b, c, d, are not coplanar then prove that a is parallel to the vector 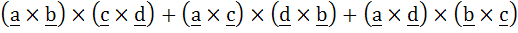
|
IIT 1994 |
|
|
758 |
Prove by vector method or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the mid points of the parallel sides (you may assume that the trapezium is not a parallelogram)
Prove by vector method or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the mid points of the parallel sides (you may assume that the trapezium is not a parallelogram)
|
IIT 1998 |
|
|
759 |
True / False Let 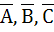 are unit vectors. Suppose that are unit vectors. Suppose that 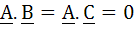 and the angle between B and and the angle between B and 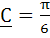 then then 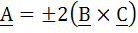 a) True b) False
True / False Let 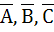 are unit vectors. Suppose that are unit vectors. Suppose that 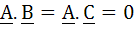 and the angle between B and and the angle between B and 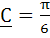 then then 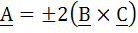 a) True b) False
|
IIT 1981 |
|
|
760 |
2sinx + tanx > 3x where 0 ≤ x ≤  a) True b) False
2sinx + tanx > 3x where 0 ≤ x ≤  a) True b) False
|
IIT 1990 |
|
|
761 |
Let f(x) = (x + 1)2 – 1, x ≥ −1 then the set {x : f(x) = f-1(x)} is a) 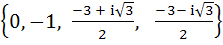 b) { 0, 1, −1} c) {0, −1} d) Ф
Let f(x) = (x + 1)2 – 1, x ≥ −1 then the set {x : f(x) = f-1(x)} is a) 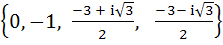 b) { 0, 1, −1} c) {0, −1} d) Ф
|
IIT 1995 |
|
|
762 |
Suppose f (x) = (x + 1)2 for x ≥ 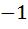 . If g (x) is the function whose graph is the reflection of the graph of f (x) with respect to the line y = x then g (x) equals . If g (x) is the function whose graph is the reflection of the graph of f (x) with respect to the line y = x then g (x) equals a) 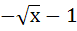 , , 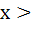 0 0 b) 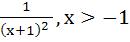 c) 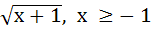 d) 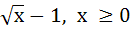
Suppose f (x) = (x + 1)2 for x ≥ 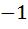 . If g (x) is the function whose graph is the reflection of the graph of f (x) with respect to the line y = x then g (x) equals . If g (x) is the function whose graph is the reflection of the graph of f (x) with respect to the line y = x then g (x) equals a) 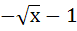 , , 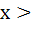 0 0 b) 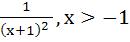 c) 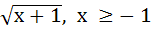 d) 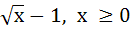
|
IIT 2000 |
|
|
763 |
Let a, b, c be three positive real numbers and
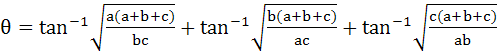
Then tan θ = ……….. a) 0 b) 1 c) 2 d) 3
Let a, b, c be three positive real numbers and
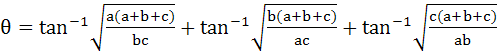
Then tan θ = ……….. a) 0 b) 1 c) 2 d) 3
|
IIT 1981 |
|
|
764 |
If X and Y are two sets and f : X 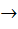 Y Y
If { f (c) = y, c ⊂ x, y ⊂ Y } then the true statement is a) 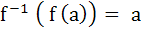 b) 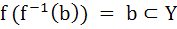 c) 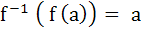 , a ⊂ X , a ⊂ X d) 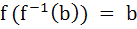
If X and Y are two sets and f : X  Y Y
If { f (c) = y, c ⊂ x, y ⊂ Y } then the true statement is a) 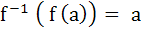 b) 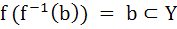 c) 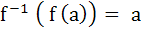 , a ⊂ X , a ⊂ X d) 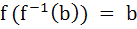
|
IIT 2005 |
|
|
765 |
Let O (0, 0), P (3, 4), Q (6, 0) be the vertices of the triangle OPQ. The point inside the triangle OPQ is such that OPR, PQR, OQR are of equal area. The coordinates of R are a) 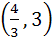 b) 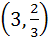 c) 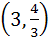 d) 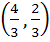
Let O (0, 0), P (3, 4), Q (6, 0) be the vertices of the triangle OPQ. The point inside the triangle OPQ is such that OPR, PQR, OQR are of equal area. The coordinates of R are a) 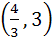 b) 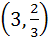 c) 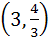 d) 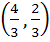
|
IIT 2006 |
|
|
766 |
If f be a one–one function with domain { x, y, z}and range { 1, 2, 3}. It is given that exactly one of the following statements is true and the remaining statements are false. Determine 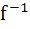 (1) (1) 1. f(x) = 1 2. f(y) ≠ 1 3. f(z) ≠ 2 a) {0} b) {1} c) {y} d) none of the above
If f be a one–one function with domain { x, y, z}and range { 1, 2, 3}. It is given that exactly one of the following statements is true and the remaining statements are false. Determine 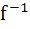 (1) (1) 1. f(x) = 1 2. f(y) ≠ 1 3. f(z) ≠ 2 a) {0} b) {1} c) {y} d) none of the above
|
IIT 1982 |
|
|
767 |
One or more correct answers
In triangle ABC the internal angle bisector of ∠A meets the side BC in D. DE is a perpendicular to AD which meets AC in E and AB in F. Then a) AE is harmonic mean of b and c b) AD 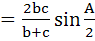 c) 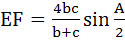 d) Δ AEF is isosceles
One or more correct answers
In triangle ABC the internal angle bisector of ∠A meets the side BC in D. DE is a perpendicular to AD which meets AC in E and AB in F. Then a) AE is harmonic mean of b and c b) AD 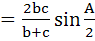 c) 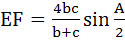 d) Δ AEF is isosceles
|
IIT 2006 |
|
|
768 |
For a triangle ABC it is given that 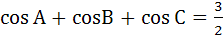 , then Δ ABC is equilateral. , then Δ ABC is equilateral. a) True b) False
For a triangle ABC it is given that 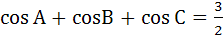 , then Δ ABC is equilateral. , then Δ ABC is equilateral. a) True b) False
|
IIT 1984 |
|
|
769 |
True / False The function f (x) = 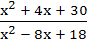 is not one to one. is not one to one. a) True b) False
True / False The function f (x) = 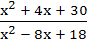 is not one to one. is not one to one. a) True b) False
|
IIT 1983 |
|
|
770 |
Find the set of all values of a such that 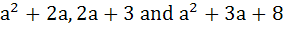 are sides of a triangle. are sides of a triangle. a) (0, 3) b) (3, ∞) c) (0, 5) d) (5, ∞)
Find the set of all values of a such that 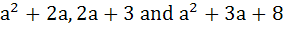 are sides of a triangle. are sides of a triangle. a) (0, 3) b) (3, ∞) c) (0, 5) d) (5, ∞)
|
IIT 1985 |
|
|
771 |
Fill in the blank Let A be the set of n distinct elements then the total number of distinct functions from A to A is ……… and out of these …… are onto a) n!, 1 b) nn, n! c) nn, 1 d) none of the above
Fill in the blank Let A be the set of n distinct elements then the total number of distinct functions from A to A is ……… and out of these …… are onto a) n!, 1 b) nn, n! c) nn, 1 d) none of the above
|
IIT 1985 |
|
|
772 |
In a triangle of base a the ratio of the other two sides is r (< 1). Then the altitude of the triangle is less than or equal to 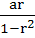 . . a) True b) False
In a triangle of base a the ratio of the other two sides is r (< 1). Then the altitude of the triangle is less than or equal to 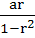 . . a) True b) False
|
IIT 1991 |
|
|
773 |
The value of k such that 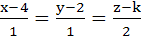 lies in the plane lies in the plane
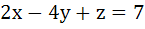 is is a) 7 b) – 7 c) No real value d) 4
The value of k such that 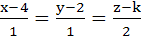 lies in the plane lies in the plane
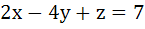 is is a) 7 b) – 7 c) No real value d) 4
|
IIT 2003 |
|
|
774 |
If ABCD are four points in a space, prove that
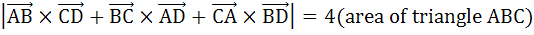
If ABCD are four points in a space, prove that
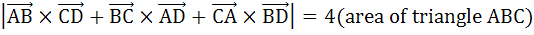
|
IIT 1987 |
|
|
775 |
If a, b, c are distinct positive numbers then the expression
( b + c – a ) ( c + a – b ) ( a + b – c ) –abc is a) Positive b) Negative c) Non–positive d) None of these
If a, b, c are distinct positive numbers then the expression
( b + c – a ) ( c + a – b ) ( a + b – c ) –abc is a) Positive b) Negative c) Non–positive d) None of these
|
IIT 1986 |
|