|
701 |
Let the vectors 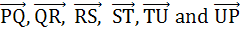 represent the edges of a regular hexagon represent the edges of a regular hexagon Statement 1 - 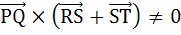 because because Statement 2 - 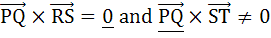 a) Statement 1 and 2 are true and Statement 2 is a correct explanation of statement 1. b) Statement 1 and 2 are true and Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
Let the vectors 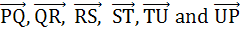 represent the edges of a regular hexagon represent the edges of a regular hexagon Statement 1 - 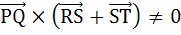 because because Statement 2 - 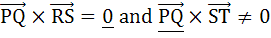 a) Statement 1 and 2 are true and Statement 2 is a correct explanation of statement 1. b) Statement 1 and 2 are true and Statement 2 is not a correct explanation of statement 1. c) Statement 1 is true. Statement 2 is false. d) Statement 1 is false. Statement 2 is true.
|
IIT 2007 |
|
|
702 |
Find the smallest possible value of p for which the equation
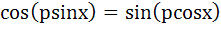 a) 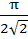 b) 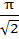 c)  d) 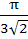
Find the smallest possible value of p for which the equation
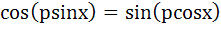 a) 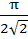 b) 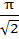 c)  d) 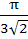
|
IIT 1995 |
|
|
703 |
If f (x) = 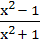 for every real x then the minimum value of f for every real x then the minimum value of f a) does not exist because f is unbounded b) is not attained even though f is bounded c) is equal to 1 d) is equal to −1
If f (x) = 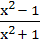 for every real x then the minimum value of f for every real x then the minimum value of f a) does not exist because f is unbounded b) is not attained even though f is bounded c) is equal to 1 d) is equal to −1
|
IIT 1998 |
|
|
704 |
Find the larger of cos(lnθ) and ln(cosθ) if 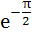 < θ < < θ <  . . a) cos(lnθ) b) ln(cosθ) c) Neither is larger throughout the interval
Find the larger of cos(lnθ) and ln(cosθ) if 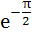 < θ < < θ <  . . a) cos(lnθ) b) ln(cosθ) c) Neither is larger throughout the interval
|
IIT 1983 |
|
|
705 |
If the function f : [ 1, 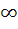 ) → [ 1, ) → [ 1, 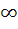 ) is defined by f (x) = 2x(x – 1) then ) is defined by f (x) = 2x(x – 1) then
f -1(x) is a) 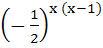 b)  ( (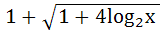 ) ) c)  ( (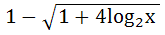 ) ) d) 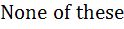
|
IIT 1999 |
|
|
706 |
If 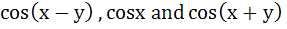 are in harmonic progression then are in harmonic progression then 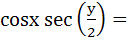 ………… ………… a) 1 b) 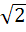 c) 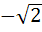 d) 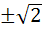
If 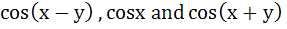 are in harmonic progression then are in harmonic progression then 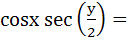 ………… ………… a) 1 b) 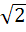 c) 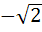 d) 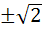
|
IIT 1997 |
|
|
707 |
If 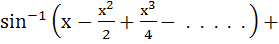 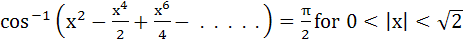
then x equals a)  b) 1 c) 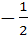 d) –1
If 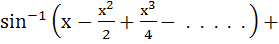 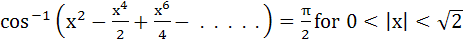
then x equals a)  b) 1 c) 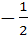 d) –1
|
IIT 1999 |
|
|
708 |
Let f ( x ) = 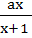 , x ≠ , x ≠ 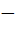 1 then for what value of a is f ( f (x)) = x 1 then for what value of a is f ( f (x)) = x a) 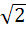 b) 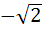 c) 1 d) 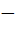 1 1
Let f ( x ) = 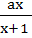 , x ≠ , x ≠ 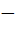 1 then for what value of a is f ( f (x)) = x 1 then for what value of a is f ( f (x)) = x a) 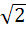 b) 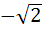 c) 1 d) 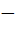 1 1
|
IIT 2001 |
|
|
709 |
If f : [ 0, 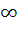 ) ) 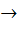 [ 0, [ 0, 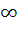 ) and f (x) = ) and f (x) = 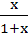 then f is then f is a) one-one and onto b) one-one but not onto c) onto but not one-one d) neither one-one nor onto
If f : [ 0, 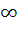 ) )  [ 0, [ 0, 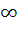 ) and f (x) = ) and f (x) = 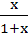 then f is then f is a) one-one and onto b) one-one but not onto c) onto but not one-one d) neither one-one nor onto
|
IIT 2003 |
|
|
710 |
Match the following Let (x, y) be such that 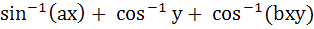 = = 
| Column 1 | Column 2 | | i) If a=1 and b=0 then (x, y) | A)Lies on the circle
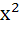 + +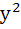 =1 =1 | | ii) If a=1 and b=1 then (x, y) | B)Lies on
(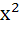 −1)( −1)(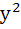 −1) = 0 −1) = 0 | | iii) If a=1 and b=2 then (x, y) | C)Lies on y = x | | iv) If a=2 and b=2 then (x, y) | D)Lies on
(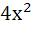 −1)( −1)(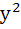 −1) = 0 −1) = 0 |
Match the following Let (x, y) be such that 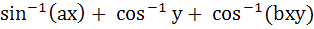 = = 
| Column 1 | Column 2 | | i) If a=1 and b=0 then (x, y) | A)Lies on the circle
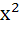 + +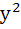 =1 =1 | | ii) If a=1 and b=1 then (x, y) | B)Lies on
(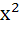 −1)( −1)(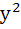 −1) = 0 −1) = 0 | | iii) If a=1 and b=2 then (x, y) | C)Lies on y = x | | iv) If a=2 and b=2 then (x, y) | D)Lies on
(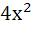 −1)( −1)(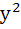 −1) = 0 −1) = 0 |
|
IIT 2007 |
|
|
711 |
f (x) = 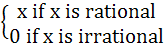
and g (x) = 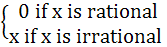
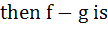 a) neither one-one nor onto b) one-one and onto c) one-one and into d) many one and onto
f (x) = 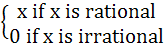
and g (x) = 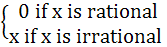
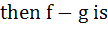 a) neither one-one nor onto b) one-one and onto c) one-one and into d) many one and onto
|
IIT 2005 |
|
|
712 |
One angle of an isosceles triangle is 120 and the radius of its incircle = and the radius of its incircle = 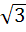 . Then the area of the triangle in square units is . Then the area of the triangle in square units is a) 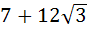 b) 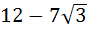 c) 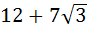 d) 2π
One angle of an isosceles triangle is 120 and the radius of its incircle = and the radius of its incircle = 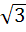 . Then the area of the triangle in square units is . Then the area of the triangle in square units is a) 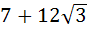 b) 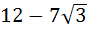 c) 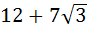 d) 2π
|
IIT 2006 |
|
|
713 |
The sides of a triangle are three consecutive natural numbers and its largest angle is twice the smallest one. Determine the sides of triangle. a) 3, 4, 5 b) 4, 5, 6 c) 4, 5, 7 d) 5, 6, 7
The sides of a triangle are three consecutive natural numbers and its largest angle is twice the smallest one. Determine the sides of triangle. a) 3, 4, 5 b) 4, 5, 6 c) 4, 5, 7 d) 5, 6, 7
|
IIT 1991 |
|
|
714 |
A plane which is perpendicular to two planes 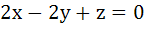 and and 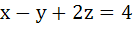 passes through (1, −2, 1). The distance of the plane from the point (1, 2, 2) is passes through (1, −2, 1). The distance of the plane from the point (1, 2, 2) is a) 0 b) 1 c) 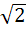 d) 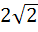
A plane which is perpendicular to two planes 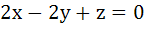 and and 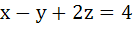 passes through (1, −2, 1). The distance of the plane from the point (1, 2, 2) is passes through (1, −2, 1). The distance of the plane from the point (1, 2, 2) is a) 0 b) 1 c) 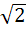 d) 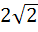
|
IIT 2006 |
|
|
715 |
Two lines having direction ratios (1, 0, −1) and (1, −1, 0) are parallel to a plane passing through (1, 1, 1). This plane cuts the coordinate axes at A, B, C. Find the value of the tetrahedron OABC.
Two lines having direction ratios (1, 0, −1) and (1, −1, 0) are parallel to a plane passing through (1, 1, 1). This plane cuts the coordinate axes at A, B, C. Find the value of the tetrahedron OABC.
|
IIT 2004 |
|
|
716 |
Let a, b, c be real numbers. Then the following system of equations in x, y, z 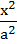 + +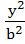 − − 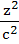 = 1 = 1 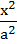 − −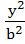 + + 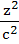 = 1 = 1 − 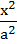 + +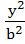 + + 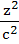 = 1 has = 1 has a) No solution b) Unique solution c) Infinitely many solutions d) Finitely many solutions
Let a, b, c be real numbers. Then the following system of equations in x, y, z 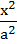 + +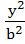 − − 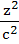 = 1 = 1 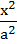 − −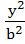 + + 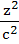 = 1 = 1 − 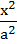 + +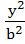 + + 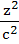 = 1 has = 1 has a) No solution b) Unique solution c) Infinitely many solutions d) Finitely many solutions
|
IIT 1995 |
|
|
717 |
Consider the lines 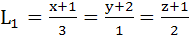 ; ;
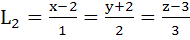
The distance of the point (1, 1, 1) from the plane through the point (−1, −2, −1) and whose normal is perpendicular to both lines L1 and L2 is
a) 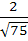 b) 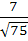 c) 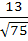 d) 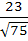
Consider the lines 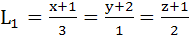 ; ;
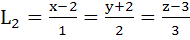
The distance of the point (1, 1, 1) from the plane through the point (−1, −2, −1) and whose normal is perpendicular to both lines L1 and L2 is
a) 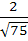 b) 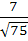 c) 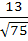 d) 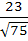
|
IIT 2008 |
|
|
718 |
The domain of definition of the function 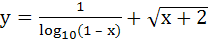 is is a) 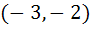 excluding excluding 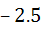 b) [0, 1] excluding 0.5 c) 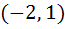 excluding x = 0 excluding x = 0 d) None of these
The domain of definition of the function 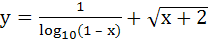 is is a) 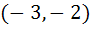 excluding excluding 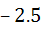 b) [0, 1] excluding 0.5 c) 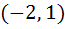 excluding x = 0 excluding x = 0 d) None of these
|
IIT 1983 |
|
|
719 |
A curve 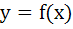 passes through passes through 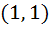 and the tangent at and the tangent at 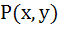 cuts the X-axis and Y-axis at A and B respectively such that cuts the X-axis and Y-axis at A and B respectively such that 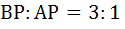 then then a) Equation of the curve is 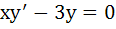 b) Normal at 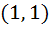 is is 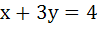 c) Curve passes through 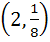 d) Equation of the curve is 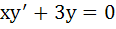
|
IIT 2006 |
|
|
720 |
Let y = f (x) be a curve passing through (1, 1) such that the triangle formed by the coordinate axes and the tangent at any point of the curve lies in the first quadrant and has area 2. Find the differential equation and determine all such possible curves.
Let y = f (x) be a curve passing through (1, 1) such that the triangle formed by the coordinate axes and the tangent at any point of the curve lies in the first quadrant and has area 2. Find the differential equation and determine all such possible curves.
|
IIT 1995 |
|
|
721 |
If 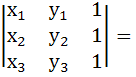 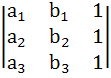
then the two triangles with vertices (x1, y1), (x2, y2), (x3, y3), and (a1, b1), (a2, b2), (a3, b3) must be congruent. a) True b) False
If 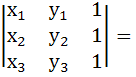 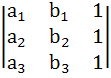
then the two triangles with vertices (x1, y1), (x2, y2), (x3, y3), and (a1, b1), (a2, b2), (a3, b3) must be congruent. a) True b) False
|
IIT 1985 |
|
|
722 |
If 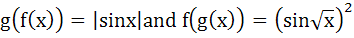 then then a) 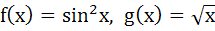 b) 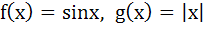 c) 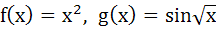 d) f and g cannot be determined
If 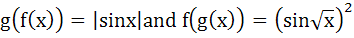 then then a) 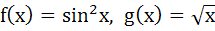 b) 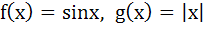 c) 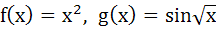 d) f and g cannot be determined
|
IIT 1998 |
|
|
723 |
A curve passes through 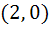 and slope at the point and slope at the point 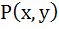 is is 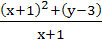 . Find the equation of the curve and the area between the . Find the equation of the curve and the area between the
curve and the X-axis in the fourth quadrant.
A curve passes through 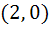 and slope at the point and slope at the point 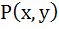 is is 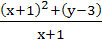 . Find the equation of the curve and the area between the . Find the equation of the curve and the area between the
curve and the X-axis in the fourth quadrant.
|
IIT 2004 |
|
|
724 |
Find the integral solutions of the following system of inequality
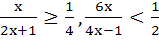 a) Ø b) x = 1 c) x = 2 d) x = 3
Find the integral solutions of the following system of inequality
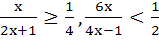 a) Ø b) x = 1 c) x = 2 d) x = 3
|
IIT 1979 |
|
|
725 |
Cosine of angle of intersection of curve y = 3x – 1lnx and y = xx – 1 is
Cosine of angle of intersection of curve y = 3x – 1lnx and y = xx – 1 is
|
IIT 2006 |
|