|
676 |
The harmonic means of the roots of the equation
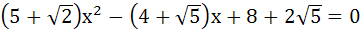 is is a) 2 b) 4 c) 6 d) 8
The harmonic means of the roots of the equation
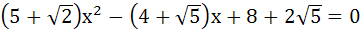 is is a) 2 b) 4 c) 6 d) 8
|
IIT 1999 |
01:43 min
|
|
677 |
Find the integral of 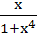 a) tan−1x2 + c b) 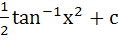 c) 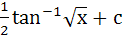 d) 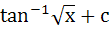
Find the integral of 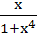 a) tan−1x2 + c b) 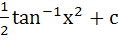 c) 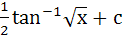 d) 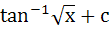
|
IIT 1978 |
00:32 min
|
|
678 |
Consider the two curves 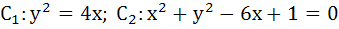 then then a) 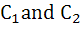 touch each other at only one point touch each other at only one point b) 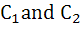 touch each other exactly at two points touch each other exactly at two points c) 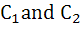 intersect(but not touch) at exactly two points intersect(but not touch) at exactly two points d) 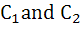 neither intersect nor touch each other neither intersect nor touch each other
Consider the two curves 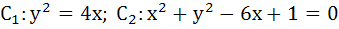 then then a) 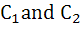 touch each other at only one point touch each other at only one point b) 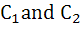 touch each other exactly at two points touch each other exactly at two points c) 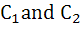 intersect(but not touch) at exactly two points intersect(but not touch) at exactly two points d) 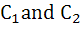 neither intersect nor touch each other neither intersect nor touch each other
|
IIT 2008 |
04:50 min
|
|
679 |
Suppose p(x) = 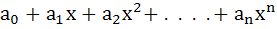
If 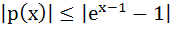 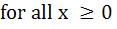 prove that prove that
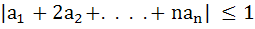
|
IIT 2000 |
05:19 min
|
|
680 |
The sum of the first 2n terms of the Arithmetic Progression 2, 5, 8, . . . . is equal to the sum of the first n terms of the Arithmetic Progression 57, 59, 61, . . . . then n equals a) 100 b) 12 c) 11 d) 13
The sum of the first 2n terms of the Arithmetic Progression 2, 5, 8, . . . . is equal to the sum of the first n terms of the Arithmetic Progression 57, 59, 61, . . . . then n equals a) 100 b) 12 c) 11 d) 13
|
IIT 2001 |
01:42 min
|
|
681 |
Show that 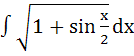 = = 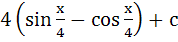
Show that 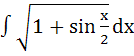 = = 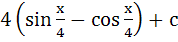
|
IIT 1980 |
01:51 min
|
|
682 |
Seven white balls and three black balls are randomly placed in a row. The possibility that no two black balls are placed adjacently equals a)  b) 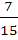 c) 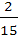 d) 
Seven white balls and three black balls are randomly placed in a row. The possibility that no two black balls are placed adjacently equals a)  b) 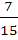 c) 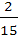 d) 
|
IIT 1998 |
03:25 min
|
|
683 |
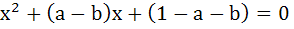 where a, b ε R then find the value of a for which equation has unequal roots for all values of b. where a, b ε R then find the value of a for which equation has unequal roots for all values of b.
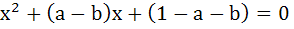 where a, b ε R then find the value of a for which equation has unequal roots for all values of b. where a, b ε R then find the value of a for which equation has unequal roots for all values of b.
|
IIT 2003 |
02:36 min
|
|
684 |
If α, β are roots of 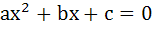 and and 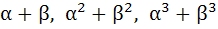 are in Geometric Progression and are in Geometric Progression and 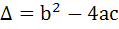 then then a) 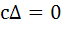 b) 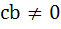 c) 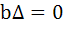 d) 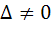
If α, β are roots of 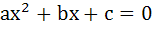 and and 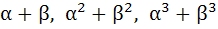 are in Geometric Progression and are in Geometric Progression and 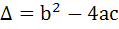 then then a) 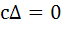 b) 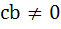 c) 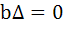 d) 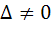
|
IIT 2005 |
02:38 min
|
|
685 |
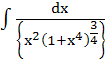 = =
a) 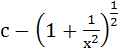 b) 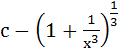 c) 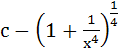 d) 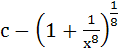
|
IIT 1984 |
02:26 min
|
|
686 |
A fair coin is tossed repeatedly. If the tail appears on first four times, then the probability of the head appearing on in the fifth toss equals a)  b) 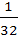 c) 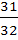 d) 
A fair coin is tossed repeatedly. If the tail appears on first four times, then the probability of the head appearing on in the fifth toss equals a)  b) 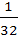 c) 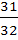 d) 
|
IIT 1998 |
00:47 min
|
|
687 |
If x and y are positive real numbers and m and n are any positive integers then 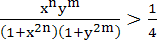
a) True b) False
If x and y are positive real numbers and m and n are any positive integers then 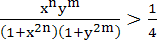
a) True b) False
|
IIT 1989 |
02:49 min
|
|
688 |
If x, y, z are in Harmonic Progression then show that
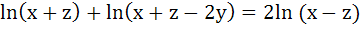
If x, y, z are in Harmonic Progression then show that
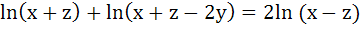
|
IIT 1978 |
02:51 min
|
|
689 |
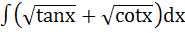 = =
a) 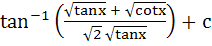 b) 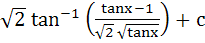 c) 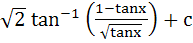 d) 
|
IIT 1989 |
04:05 min
|
|
690 |
The points with position vectors 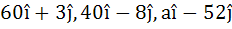 are collinear if are collinear if a) 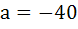 b) 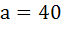 c) 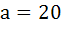 d) 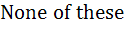
The points with position vectors 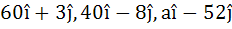 are collinear if are collinear if a) 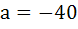 b) 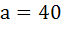 c) 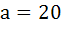 d) 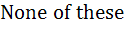
|
IIT 1983 |
03:14 min
|
|
691 |
If P (B) = 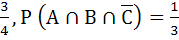 and and 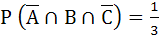 then then P (B ∩ C) is a) 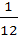 b)  c) 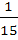 d) 
If P (B) = 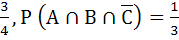 and and 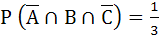 then then P (B ∩ C) is a) 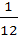 b)  c) 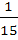 d) 
|
IIT 2004 |
02:56 min
|
|
692 |
Fill in the blank The solution of the equation
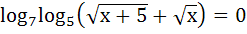 is ………….. is …………..
Fill in the blank The solution of the equation
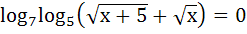 is ………….. is …………..
|
IIT 1986 |
02:04 min
|
|
693 |
Let 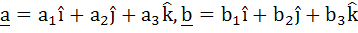 and and 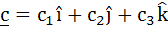 be three non-zero vectors such that c is a unit vector perpendicular to both the vectors a and b and the angle between the vectors a and b is be three non-zero vectors such that c is a unit vector perpendicular to both the vectors a and b and the angle between the vectors a and b is  then then
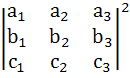 is equal to is equal to a) 1 b) 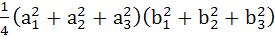 c) 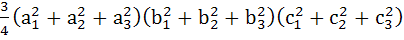 d) None of these
Let 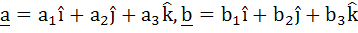 and and 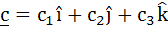 be three non-zero vectors such that c is a unit vector perpendicular to both the vectors a and b and the angle between the vectors a and b is be three non-zero vectors such that c is a unit vector perpendicular to both the vectors a and b and the angle between the vectors a and b is  then then
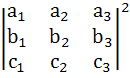 is equal to is equal to a) 1 b) 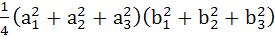 c) 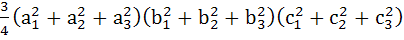 d) None of these
|
IIT 1986 |
|
|
694 |
Does there exist a Geometric Progression containing 27, 8 and 12 as three of its terms? If it exists, how many such progressions are possible?
Does there exist a Geometric Progression containing 27, 8 and 12 as three of its terms? If it exists, how many such progressions are possible?
|
IIT 1982 |
|
|
695 |
The values of 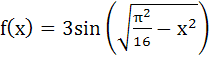 lies in the interval . . . lies in the interval . . .
The values of 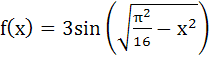 lies in the interval . . . lies in the interval . . .
|
IIT 1983 |
|
|
696 |
If 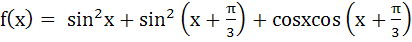 and and 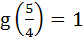 then (gof)(x) is equal to then (gof)(x) is equal to
If 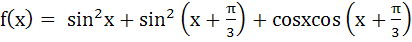 and and 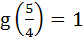 then (gof)(x) is equal to then (gof)(x) is equal to
|
IIT 1996 |
|
|
697 |
If 0 < x < 1, then 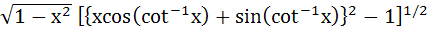 is equal to is equal to
If 0 < x < 1, then 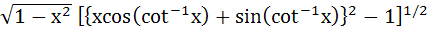 is equal to is equal to
|
IIT 2008 |
|
|
698 |
The sum of integers from 1 to 100 that are divisible by 2 or 5 is
The sum of integers from 1 to 100 that are divisible by 2 or 5 is
|
IIT 1984 |
|
|
699 |
The minimum value of the expression 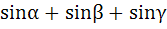 where where 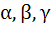 are real numbers satisfying are real numbers satisfying 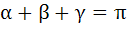 is is a) Positive b) Zero c) Negative d) –3
The minimum value of the expression 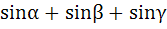 where where 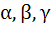 are real numbers satisfying are real numbers satisfying 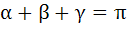 is is a) Positive b) Zero c) Negative d) –3
|
IIT 1995 |
|
|
700 |
Using the relation 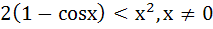 , or otherwise prove that , or otherwise prove that 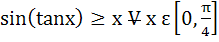 a) True b) False
Using the relation 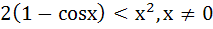 , or otherwise prove that , or otherwise prove that 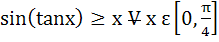 a) True b) False
|
IIT 2003 |
|