|
626 |
For a ≤ 0, determine all real roots of the equation
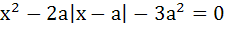
For a ≤ 0, determine all real roots of the equation
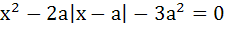
|
IIT 1986 |
03:49 min
|
|
627 |
If a, b, c, d and p are distinct real numbers such that
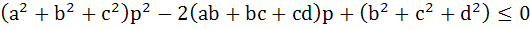
then a, b, c, d a) Are in Arithmetic Progression b) Are in Geometric Progression c) Are in Harmonic Progression d) Satisfy ab = cd e) Satisfy none of these
If a, b, c, d and p are distinct real numbers such that
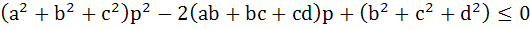
then a, b, c, d a) Are in Arithmetic Progression b) Are in Geometric Progression c) Are in Harmonic Progression d) Satisfy ab = cd e) Satisfy none of these
|
IIT 1987 |
02:16 min
|
|
628 |
Suppose f(x) is a function satisfying the following conditions i) f(0) = 2, f(1) = 1 ii) f has a minimum value at x = 5/2 and iii) for all x 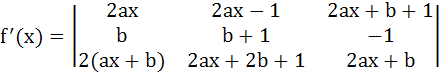
where a, b are constants. Determine the constants a and b, and the function f(x).
a) 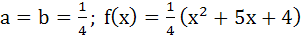 b) 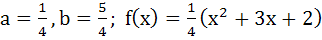 c) 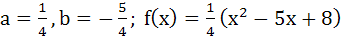 d) 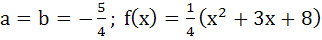
Suppose f(x) is a function satisfying the following conditions i) f(0) = 2, f(1) = 1 ii) f has a minimum value at x = 5/2 and iii) for all x 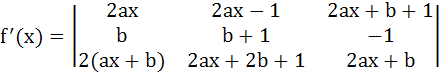
where a, b are constants. Determine the constants a and b, and the function f(x).
a) 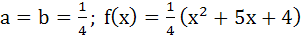 b) 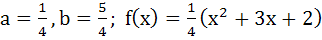 c) 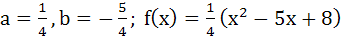 d) 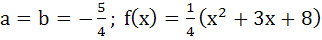
|
IIT 1998 |
06:16 min
|
|
629 |
Solve 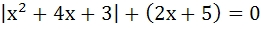
Solve 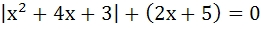
|
IIT 1988 |
03:54 min
|
|
630 |
If 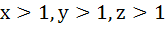 are in Geometric Progression then are in Geometric Progression then
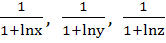 are in are in a) Arithmetic Progression b) Geometric Progression c) Harmonic Progression d) None of these
If 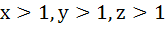 are in Geometric Progression then are in Geometric Progression then
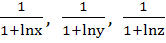 are in are in a) Arithmetic Progression b) Geometric Progression c) Harmonic Progression d) None of these
|
IIT 1998 |
02:25 min
|
|
631 |
Let 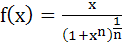 for n ≥ 2 and for n ≥ 2 and
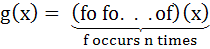 Then 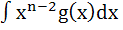 equals equals a) 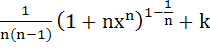 b) 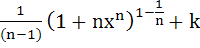 c) 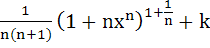 d) 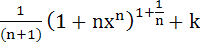
Let 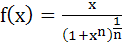 for n ≥ 2 and for n ≥ 2 and
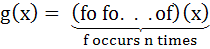 Then 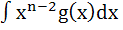 equals equals a) 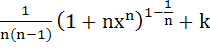 b) 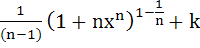 c) 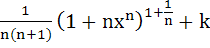 d) 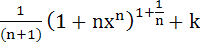
|
IIT 2007 |
08:22 min
|
|
632 |
India played two matches each with Australia and West indies. In any match the probability of India getting the points 0, 1, and 2 are 0.45, 0.05 and 0.50 respectively. Assuming that the outcomes are independent, the probability of India getting at least seven points is a) 0.8730 b) 0.0875 c) 0.0625 d) 0.0250
India played two matches each with Australia and West indies. In any match the probability of India getting the points 0, 1, and 2 are 0.45, 0.05 and 0.50 respectively. Assuming that the outcomes are independent, the probability of India getting at least seven points is a) 0.8730 b) 0.0875 c) 0.0625 d) 0.0250
|
IIT 1992 |
03:03 min
|
|
633 |
Let Tn denote the number of triangles which can be formed using the vertices of a regular polygon of n sides. If 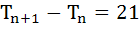 then n equals then n equals a) 5 b) 7 c) 6 d) 4
Let Tn denote the number of triangles which can be formed using the vertices of a regular polygon of n sides. If 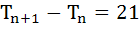 then n equals then n equals a) 5 b) 7 c) 6 d) 4
|
IIT 2001 |
02:30 min
|
|
634 |
Three of the vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral equals a)  b)  c) 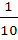 d) 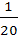
Three of the vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral equals a)  b)  c) 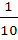 d) 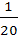
|
IIT 1995 |
02:30 min
|
|
635 |
Let a, b, c be real numbers with a ≠ 0 and let α, β be roots of the equation 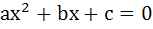 . Express the roots of . Express the roots of 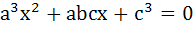 in terms of α, β. in terms of α, β.
Let a, b, c be real numbers with a ≠ 0 and let α, β be roots of the equation 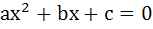 . Express the roots of . Express the roots of 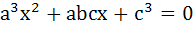 in terms of α, β. in terms of α, β.
|
IIT 2001 |
04:00 min
|
|
636 |
Suppose a, b, c are in Arithmetic Progression and 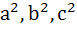 are in Geometric Progression. If are in Geometric Progression. If 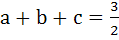 then the value of a is then the value of a is a) 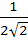 b) 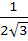 c) 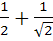 d) 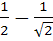
Suppose a, b, c are in Arithmetic Progression and 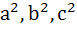 are in Geometric Progression. If are in Geometric Progression. If 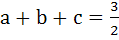 then the value of a is then the value of a is a) 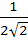 b) 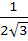 c) 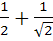 d) 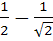
|
IIT 2002 |
05:17 min
|
|
637 |
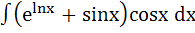 = =
a) 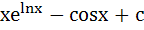 b) 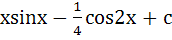 c) 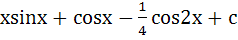 d) 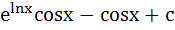
|
IIT 1981 |
00:56 min
|
|
638 |
If 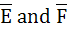 are complementary events E and F respectively and if 0 < p(E) < 1, then are complementary events E and F respectively and if 0 < p(E) < 1, then a) 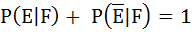 b) 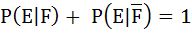 c) 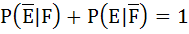 d) 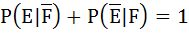
If 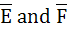 are complementary events E and F respectively and if 0 < p(E) < 1, then are complementary events E and F respectively and if 0 < p(E) < 1, then a) 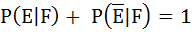 b) 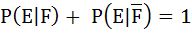 c) 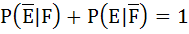 d) 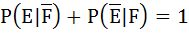
|
IIT 1998 |
01:47 min
|
|
639 |
The equation 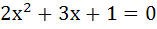 has an irrational root. has an irrational root. a) False b) True
The equation 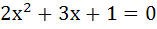 has an irrational root. has an irrational root. a) False b) True
|
IIT 1983 |
00:48 min
|
|
640 |
Multiple Choice For 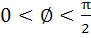 if if
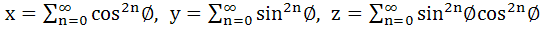 , then , then a) 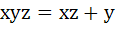 b) 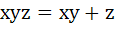 c) 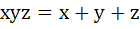 d) 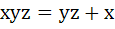
Multiple Choice For 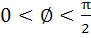 if if
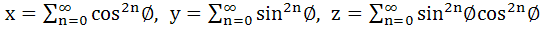 , then , then a) 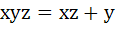 b) 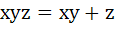 c) 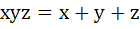 d) 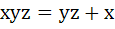
|
IIT 1993 |
06:15 min
|
|
641 |
The numbers are selected from the set S = {1, 2, 3, 4, 5, 6} without replacement one by one. Probability that the minimum of the two numbers is less than 4 is a) 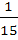 b) 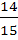 c)  d) 
The numbers are selected from the set S = {1, 2, 3, 4, 5, 6} without replacement one by one. Probability that the minimum of the two numbers is less than 4 is a) 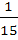 b) 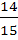 c)  d) 
|
IIT 2003 |
03:06 min
|
|
642 |
Fill in the blank If the product of the roots of the equation
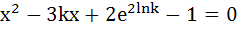 is 7 is 7
Then the roots are real for 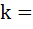 …………. ………….
Fill in the blank If the product of the roots of the equation
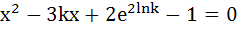 is 7 is 7
Then the roots are real for 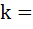 …………. ………….
|
IIT 1984 |
01:40 min
|
|
643 |
Show that the integral
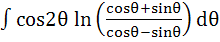 = = 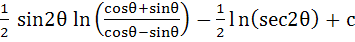
Show that the integral
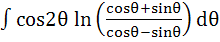 = = 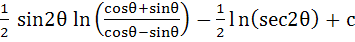
|
IIT 1994 |
06:09 min
|
|
644 |
One Indian and four American men and their wives are to be seated randomly around a circular table. Then the conditional probability that Indian man is seated adjacent to his wife given that each American man is seated adjacent to his wife is a)  b)  c)  d) 
One Indian and four American men and their wives are to be seated randomly around a circular table. Then the conditional probability that Indian man is seated adjacent to his wife given that each American man is seated adjacent to his wife is a)  b)  c)  d) 
|
IIT 2007 |
09:20 min
|
|
645 |
Fill in the blank There are exactly two distinct linear functions ………. and ………. which map {−1, 1} onto {0, 2}.
Fill in the blank There are exactly two distinct linear functions ………. and ………. which map {−1, 1} onto {0, 2}.
|
IIT 1989 |
02:15 min
|
|
646 |
Find three numbers a, b, c between 2 and 18 such that (i) their sum is 25 (ii) 2, a, b are consecutive terms of an Arithmetic Progression and (iii) the numbers b, c, 18 are consecutive terms of a Geometric Progression
Find three numbers a, b, c between 2 and 18 such that (i) their sum is 25 (ii) 2, a, b are consecutive terms of an Arithmetic Progression and (iii) the numbers b, c, 18 are consecutive terms of a Geometric Progression
|
IIT 1983 |
04:09 min
|
|
647 |
Show that 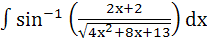 = =
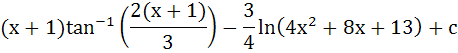
Show that 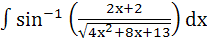 = =
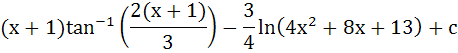
|
IIT 2001 |
06:38 min
|
|
648 |
Let p and q be the position vectors of P and Q respectively with respect to O and 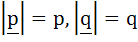 . The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If OR and OS are perpendicular then . The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If OR and OS are perpendicular then a) 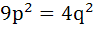 b) 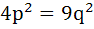 c) 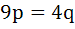 d) 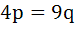
Let p and q be the position vectors of P and Q respectively with respect to O and 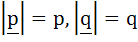 . The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If OR and OS are perpendicular then . The points R and S divide PQ internally and externally in the ratio 2:3 respectively. If OR and OS are perpendicular then a) 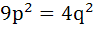 b) 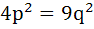 c) 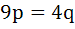 d) 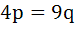
|
IIT 1994 |
02:26 min
|
|
649 |
Let u, v and w be vectors such that 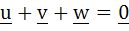 . If . If 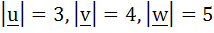 then then 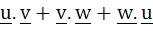 is equal to is equal to a) 47 b) –25 c) 0 d) 25
Let u, v and w be vectors such that 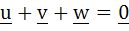 . If . If 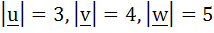 then then 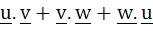 is equal to is equal to a) 47 b) –25 c) 0 d) 25
|
IIT 1995 |
05:00 min
|
|
650 |
(One or more correct answers)
There are four machines and it is known that exactly two of them are faulty. They are tested one by one, in a random order till both the faulty machines are identified. Then the probability that only two tests are needed a)  b)  c)  d) 
(One or more correct answers)
There are four machines and it is known that exactly two of them are faulty. They are tested one by one, in a random order till both the faulty machines are identified. Then the probability that only two tests are needed a)  b)  c)  d) 
|
IIT 1998 |
04:38 min
|