|
526 |
If two distinct chords drawn from the point (p, q) on the circle 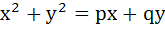 (where pq ≠ 0) are bisected by the X-axis then (where pq ≠ 0) are bisected by the X-axis then a) 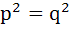 b) 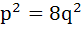 c) 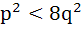 d) 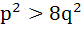
If two distinct chords drawn from the point (p, q) on the circle 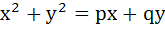 (where pq ≠ 0) are bisected by the X-axis then (where pq ≠ 0) are bisected by the X-axis then a) 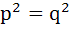 b) 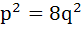 c) 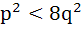 d) 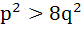
|
IIT 1999 |
05:52 min
|
|
527 |
Let 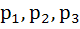 are the perpendiculars from the vertices of a triangle to the opposite sides, then are the perpendiculars from the vertices of a triangle to the opposite sides, then 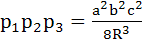 a) True b) False
Let 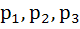 are the perpendiculars from the vertices of a triangle to the opposite sides, then are the perpendiculars from the vertices of a triangle to the opposite sides, then 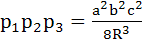 a) True b) False
|
IIT 1978 |
02:41 min
|
|
528 |
The coefficient of x99 in the polynomial
(x – 1) (x – 2) . . . (x – 100) is
The coefficient of x99 in the polynomial
(x – 1) (x – 2) . . . (x – 100) is
|
IIT 1982 |
02:12 min
|
|
529 |
Evaluate 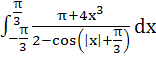
Evaluate 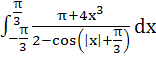
|
IIT 2004 |
07:21 min
|
|
530 |
The sum of the rational terms in the expansion of 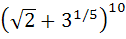 is is
The sum of the rational terms in the expansion of 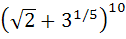 is is
|
IIT 1997 |
03:13 min
|
|
531 |
A unit vector perpendicular to the plane determined by the points P (1, -1, 2), Q (2, 0, -1) and R (0, 2, 1) is . . . . .
A unit vector perpendicular to the plane determined by the points P (1, -1, 2), Q (2, 0, -1) and R (0, 2, 1) is . . . . .
|
IIT 1994 |
03:33 min
|
|
532 |
If one of the diameters of the circle 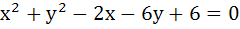 is a chord to the circle with centre (2, 1) then the radius of the circle is is a chord to the circle with centre (2, 1) then the radius of the circle is a) 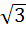 b) 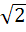 c) 3 d) 2
If one of the diameters of the circle 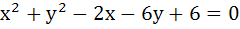 is a chord to the circle with centre (2, 1) then the radius of the circle is is a chord to the circle with centre (2, 1) then the radius of the circle is a) 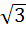 b) 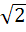 c) 3 d) 2
|
IIT 2004 |
02:47 min
|
|
533 |
Which of the following functions is periodic? a) f(x) = x – [x] where [x] denotes the greatest integer less than or equal to the real number x b) f(x) = sin 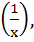 x ≠ 0, f(0) = 0 x ≠ 0, f(0) = 0 c) f(x) = x cos x d) None of these
Which of the following functions is periodic? a) f(x) = x – [x] where [x] denotes the greatest integer less than or equal to the real number x b) f(x) = sin 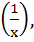 x ≠ 0, f(0) = 0 x ≠ 0, f(0) = 0 c) f(x) = x cos x d) None of these
|
IIT 1983 |
01:19 min
|
|
534 |
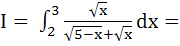
a)  b)  c) 1 d) 2
|
IIT 1994 |
01:46 min
|
|
535 |
Let a, b and c be three vectors having magnitudes 1, 1 and 2 respectively. If 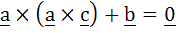 then the acute angle between a and c is . . . . . then the acute angle between a and c is . . . . .
Let a, b and c be three vectors having magnitudes 1, 1 and 2 respectively. If 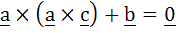 then the acute angle between a and c is . . . . . then the acute angle between a and c is . . . . .
|
IIT 1997 |
04:42 min
|
|
536 |
The equation of the tangents drawn from the origin to the circle 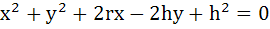 are are a) x= 6 b) y = 0 c) 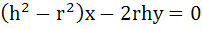 d) 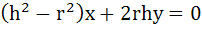
The equation of the tangents drawn from the origin to the circle 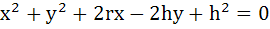 are are a) x= 6 b) y = 0 c) 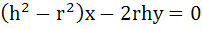 d) 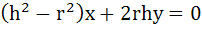
|
IIT 1988 |
04:06 min
|
|
537 |
Let f (x) be defined for all x > 0 and be continuous. If f (x) satisfies
f 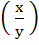 = f (x) – f (y) for all x and y and f (e) = 1 then = f (x) – f (y) for all x and y and f (e) = 1 then a) f (x) is bounded b) f 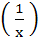 → 0 as x → 0 → 0 as x → 0 c) x f 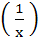 → 0 as x → 0 → 0 as x → 0 d) f (x) = lnx
Let f (x) be defined for all x > 0 and be continuous. If f (x) satisfies
f 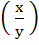 = f (x) – f (y) for all x and y and f (e) = 1 then = f (x) – f (y) for all x and y and f (e) = 1 then a) f (x) is bounded b) f 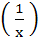 → 0 as x → 0 → 0 as x → 0 c) x f 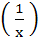 → 0 as x → 0 → 0 as x → 0 d) f (x) = lnx
|
IIT 1995 |
02:06 min
|
|
538 |
The value of 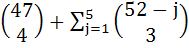 is equal to is equal to a) 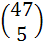 b) 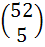 c) 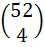 d) None of these
The value of 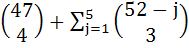 is equal to is equal to a) 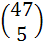 b) 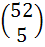 c) 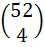 d) None of these
|
IIT 1980 |
03:48 min
|
|
539 |
The area bounded by the curve y = f(x), the X–axis and the ordinate x = 1 and x = b is (b – 1) sin (3b + 4). Then f(x) is a) (x – 1) cos (3x + 4) b) sin(3x + 4) c) sin(3x + 4) + 3(x – 1) cos (3x + 4) d) none of these
The area bounded by the curve y = f(x), the X–axis and the ordinate x = 1 and x = b is (b – 1) sin (3b + 4). Then f(x) is a) (x – 1) cos (3x + 4) b) sin(3x + 4) c) sin(3x + 4) + 3(x – 1) cos (3x + 4) d) none of these
|
IIT 1983 |
01:13 min
|
|
540 |
Through a fixed point (h, k) secants are drawn to the circle 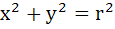 . Show that the locus of the mid points of the secant intercepted by the circle is . Show that the locus of the mid points of the secant intercepted by the circle is 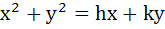
Through a fixed point (h, k) secants are drawn to the circle 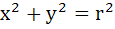 . Show that the locus of the mid points of the secant intercepted by the circle is . Show that the locus of the mid points of the secant intercepted by the circle is 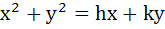
|
IIT 1983 |
02:28 min
|
|
541 |
There exists a solution of θ between 0 and 2π that satisfies the equation 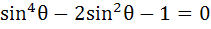 . . a) True b) False
There exists a solution of θ between 0 and 2π that satisfies the equation 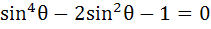 . . a) True b) False
|
IIT 1980 |
02:16 min
|
|
542 |
The number of values of x where the function
f (x) = cos x + cos (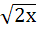 ) attains the maximum is ) attains the maximum is a) 0 b) 1 c) 2 d) Infinite
The number of values of x where the function
f (x) = cos x + cos (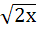 ) attains the maximum is ) attains the maximum is a) 0 b) 1 c) 2 d) Infinite
|
IIT 1998 |
01:38 min
|
|
543 |
Evaluate 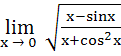 a) 0 b)  c) 1 d) 2
Evaluate 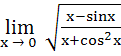 a) 0 b)  c) 1 d) 2
|
IIT 1979 |
00:54 min
|
|
544 |
The circle 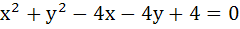 is inscribed in a triangle which has two of its sides along the co-ordinate axes. The locus of the circum centre of the triangle is is inscribed in a triangle which has two of its sides along the co-ordinate axes. The locus of the circum centre of the triangle is 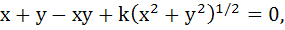 find k. find k.
The circle 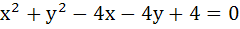 is inscribed in a triangle which has two of its sides along the co-ordinate axes. The locus of the circum centre of the triangle is is inscribed in a triangle which has two of its sides along the co-ordinate axes. The locus of the circum centre of the triangle is 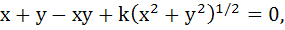 find k. find k.
|
IIT 1987 |
07:11 min
|
|
545 |
The domain of definition of the function f (x) given by the equation 2x + 2y = 2 is a) 0 < x ≤ 1 b) 0 ≤ x ≤ 1 c) 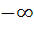 < x ≤ 0 < x ≤ 0 d) 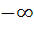 < x ≤ 1 < x ≤ 1
The domain of definition of the function f (x) given by the equation 2x + 2y = 2 is a) 0 < x ≤ 1 b) 0 ≤ x ≤ 1 c) 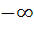 < x ≤ 0 < x ≤ 0 d) 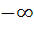 < x ≤ 1 < x ≤ 1
|
IIT 2000 |
01:23 min
|
|
546 |
Determine the values of a, b, c for which the function 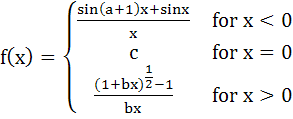
is continuous at x = 0 a) 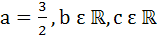 b) 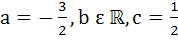 c) 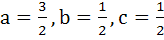 d) 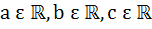
Determine the values of a, b, c for which the function 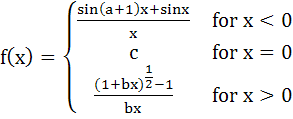
is continuous at x = 0 a) 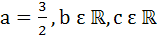 b) 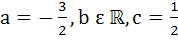 c) 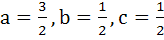 d) 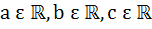
|
IIT 1982 |
04:00 min
|
|
547 |
If 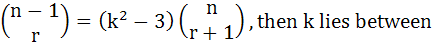 a) 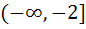 b) [2, ∞) c) 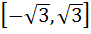 d) 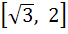
|
IIT 2002 |
06:15 min
|
|
548 |
The function 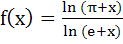 is is a) Increasing on (0, ∞) b) Decreasing on (0, ∞) c) Increasing on 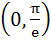 and decreasing on and decreasing on 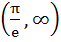 d) Increasing on 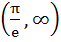 and decreasing on and decreasing on 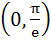
The function 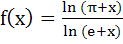 is is a) Increasing on (0, ∞) b) Decreasing on (0, ∞) c) Increasing on 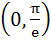 and decreasing on and decreasing on 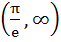 d) Increasing on 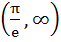 and decreasing on and decreasing on 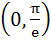
|
IIT 1995 |
02:10 min
|
|
549 |
A point P is given on the circumference of a circle of radius r. Chord QR is parallel to the tangent at P. Determine the maximum possible area of ΔPQR.
A point P is given on the circumference of a circle of radius r. Chord QR is parallel to the tangent at P. Determine the maximum possible area of ΔPQR.
|
IIT 1990 |
08:40 min
|
|
550 |
If we consider only the principal values of the inverse trigonometric functions then the value of 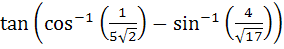 is is
a) 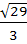 b) 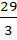 c) 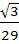 d) 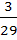
If we consider only the principal values of the inverse trigonometric functions then the value of 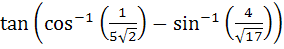 is is
a) 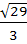 b) 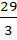 c) 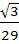 d) 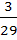
|
IIT 1994 |
02:29 min
|