|
476 |
Let f(x) be a quadratic expression which is positive for all values of x. If g(x) = 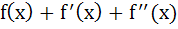 then for any real x then for any real x a) g (x) < 0 b) g (x) > 0 c) g (x) = 0 d) g (x) ≥ 0
Let f(x) be a quadratic expression which is positive for all values of x. If g(x) = 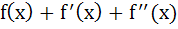 then for any real x then for any real x a) g (x) < 0 b) g (x) > 0 c) g (x) = 0 d) g (x) ≥ 0
|
IIT 1990 |
02:54 min
|
|
477 |
If 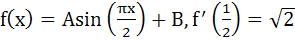 and and 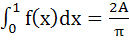 , then constants A and B are , then constants A and B are a) 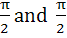 b) 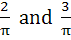 c) 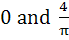 d) 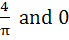
If 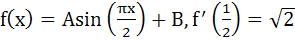 and and 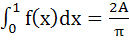 , then constants A and B are , then constants A and B are a) 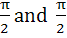 b) 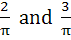 c) 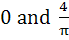 d) 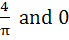
|
IIT 1995 |
02:11 min
|
|
478 |
If the vectors 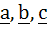 form sides BC, CA and AB respectively of a triangle ABC then form sides BC, CA and AB respectively of a triangle ABC then a) 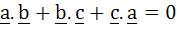 b) 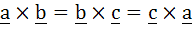 c) 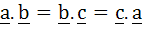 d) 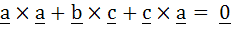
If the vectors 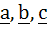 form sides BC, CA and AB respectively of a triangle ABC then form sides BC, CA and AB respectively of a triangle ABC then a) 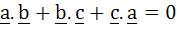 b) 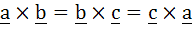 c) 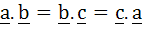 d) 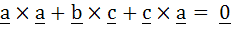
|
IIT 2000 |
02:48 min
|
|
479 |
Cards are drawn one by one at random from a well shuffled pack of 52 playing cards until 2 aces are drawn for the first time. If N is the number of cards required to be drawn show that
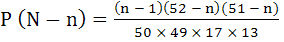 where 2 < n ≤ 50 where 2 < n ≤ 50
Cards are drawn one by one at random from a well shuffled pack of 52 playing cards until 2 aces are drawn for the first time. If N is the number of cards required to be drawn show that
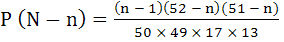 where 2 < n ≤ 50 where 2 < n ≤ 50
|
IIT 1983 |
07:44 min
|
|
480 |
If the lengths of the sides of a triangle are 3, 5, 7 then the largest angle of the triangle is a)  b) 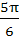 c) 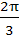 d) 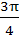
If the lengths of the sides of a triangle are 3, 5, 7 then the largest angle of the triangle is a)  b) 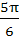 c) 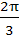 d) 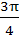
|
IIT 1994 |
01:44 min
|
|
481 |
If y = y (x) and it follows the relation xcosy + ycosx = π then 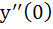 is is a) – 1 b) π c) – π d) 1
If y = y (x) and it follows the relation xcosy + ycosx = π then 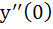 is is a) – 1 b) π c) – π d) 1
|
IIT 2005 |
03:40 min
|
|
482 |
Let f be a positive function. Let
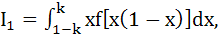
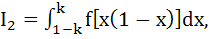 where where
2k – 1 > 0 then 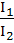 is is a) 2 b) k c)  d) 1
Let f be a positive function. Let
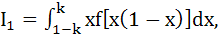
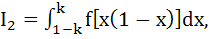 where where
2k – 1 > 0 then 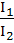 is is a) 2 b) k c)  d) 1
|
IIT 1997 |
02:23 min
|
|
483 |
Let
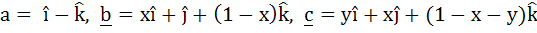 , ,
then 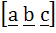 depends on depends on a) Only x b) Only y c) Neither x nor y d) Both x and y
Let
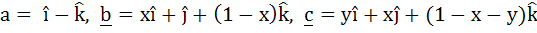 , ,
then 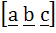 depends on depends on a) Only x b) Only y c) Neither x nor y d) Both x and y
|
IIT 2001 |
01:20 min
|
|
484 |
In a multiple choice question there are four alternative answers out of which one or more is correct. A candidate will get full marks in the question only if he ticks the correct answers. If he is allowed up to three chances to answer the question, find the probability that he will get marks in the question?
In a multiple choice question there are four alternative answers out of which one or more is correct. A candidate will get full marks in the question only if he ticks the correct answers. If he is allowed up to three chances to answer the question, find the probability that he will get marks in the question?
|
IIT 1985 |
05:36 min
|
|
485 |
Let the Harmonic Mean and Geometric Mean of two positive numbers be in the ratio of 4:5. Then the two numbers are in the ratio . . . . .
Let the Harmonic Mean and Geometric Mean of two positive numbers be in the ratio of 4:5. Then the two numbers are in the ratio . . . . .
|
IIT 1992 |
02:26 min
|
|
486 |
If f (x) = 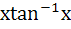 , find , find 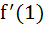 from first principle. from first principle. a) 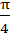 b) 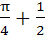 c) 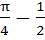 d) 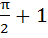
If f (x) = 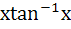 , find , find 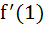 from first principle. from first principle. a) 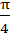 b) 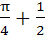 c) 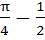 d) 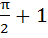
|
IIT 1978 |
04:21 min
|
|
487 |
If for real number y, [y] is the greatest integer less than or equal to y then the value of the integral 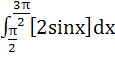 is is a) 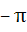 b) 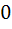 c) 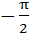 d) 
If for real number y, [y] is the greatest integer less than or equal to y then the value of the integral 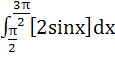 is is a) 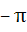 b) 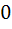 c) 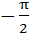 d) 
|
IIT 1999 |
07:44 min
|
|
488 |
If 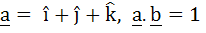 and and 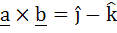 then b is equal to then b is equal to a) 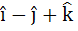 b) 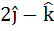 c) 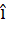 d) 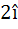
If 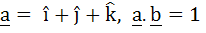 and and 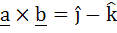 then b is equal to then b is equal to a) 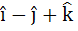 b) 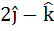 c) 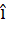 d) 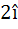
|
IIT 2004 |
02:35 min
|
|
489 |
A box contains two 50 paise coins, 5 twenty five paise coins and a certain number N(≥ 2) of ten and five paise coins. Five coins are taken out of the box at random. Find the probability that the total value of these coins is less than one rupee and 50 paise.
A box contains two 50 paise coins, 5 twenty five paise coins and a certain number N(≥ 2) of ten and five paise coins. Five coins are taken out of the box at random. Find the probability that the total value of these coins is less than one rupee and 50 paise.
|
IIT 1988 |
06:49 min
|
|
490 |
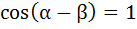 and and 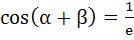
where α, β ε [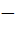 π, π]. Values of α, β which satisfy both the equations is/are π, π]. Values of α, β which satisfy both the equations is/are
a) 0 b) 1 c) 2 d) 4
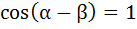 and and 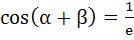
where α, β ε [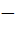 π, π]. Values of α, β which satisfy both the equations is/are π, π]. Values of α, β which satisfy both the equations is/are
a) 0 b) 1 c) 2 d) 4
|
IIT 2005 |
04:42 min
|
|
491 |
Given positive integers r > 1, n > 2 and the coefficients of (3r)th term and (r + 2)th terms in the binomial expansion of (1 + x)2n are equal then a) n = 2r b) n = 2r + 1 c) n = 3r d) none of these
Given positive integers r > 1, n > 2 and the coefficients of (3r)th term and (r + 2)th terms in the binomial expansion of (1 + x)2n are equal then a) n = 2r b) n = 2r + 1 c) n = 3r d) none of these
|
IIT 1980 |
03:03 min
|
|
492 |
The number of distinct real values of λ for which 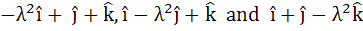 are coplanar is are coplanar is a) Zero b) One c) Two d) three
The number of distinct real values of λ for which 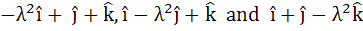 are coplanar is are coplanar is a) Zero b) One c) Two d) three
|
IIT 2007 |
03:01 min
|
|
493 |
If 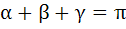 , then , then 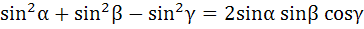 a) True b) False
If 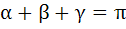 , then , then 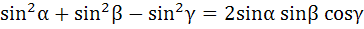 a) True b) False
|
IIT 1980 |
04:29 min
|
|
494 |
If in the expansion of (1 + x)m (1 – x)n, the coefficients of x and x2 are 3 and –6 respectively. then m is a) 6 b) 9 c) 12 d) 24
If in the expansion of (1 + x)m (1 – x)n, the coefficients of x and x2 are 3 and –6 respectively. then m is a) 6 b) 9 c) 12 d) 24
|
IIT 1999 |
04:34 min
|
|
495 |
If 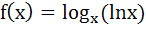 then then 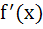 at x = e is . . . at x = e is . . . a) 0 b)  c) e d) 1
If 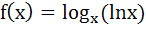 then then 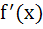 at x = e is . . . at x = e is . . . a) 0 b)  c) e d) 1
|
IIT 1985 |
01:35 min
|
|
496 |
If 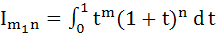 then the expression for then the expression for 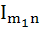 in terms of in terms of 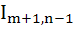 is is a) 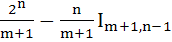 b) 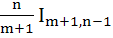 c) 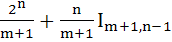 d) 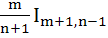
If 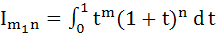 then the expression for then the expression for 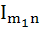 in terms of in terms of 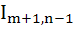 is is a) 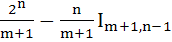 b) 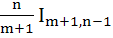 c) 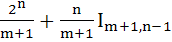 d) 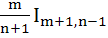
|
IIT 2003 |
01:32 min
|
|
497 |
Multiple choice Which of the following expressions are meaningful a) 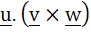 b) 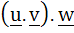 c) 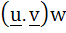 d) 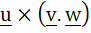
Multiple choice Which of the following expressions are meaningful a) 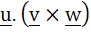 b) 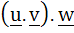 c) 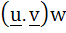 d) 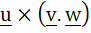
|
IIT 1998 |
01:15 min
|
|
498 |
If 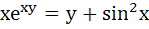 then at x = 0, then at x = 0, 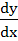 is equal to is equal to a) 0 b) 1 c) 2 d) 4
If 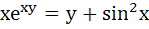 then at x = 0, then at x = 0, 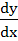 is equal to is equal to a) 0 b) 1 c) 2 d) 4
|
IIT 1996 |
02:05 min
|
|
499 |
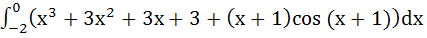 is equal to is equal to
a) 0 b) 4 c) 6 d) −4
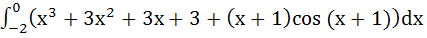 is equal to is equal to
a) 0 b) 4 c) 6 d) −4
|
IIT 2004 |
03:15 min
|
|
500 |
Find all values of λ such that 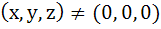 and and 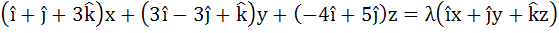 where where 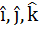 are unit vectors along the coordinate vectors. are unit vectors along the coordinate vectors.
Find all values of λ such that 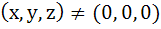 and and 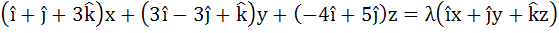 where where 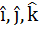 are unit vectors along the coordinate vectors. are unit vectors along the coordinate vectors.
|
IIT 1982 |
04:48 min
|