|
451 |
Multiple choices
y = f ( x ) = 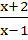 then then a) x = f (y) b) f (1) = 3 c) y is increasing with x for x < 1 d) f is a rational function of x
Multiple choices
y = f ( x ) = 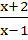 then then a) x = f (y) b) f (1) = 3 c) y is increasing with x for x < 1 d) f is a rational function of x
|
IIT 1989 |
01:29 min
|
|
452 |
A committee of 12 is to be formed from 9 women and 8 men. In how many ways this can be if at least five women have to be in the committee? In how many ways in these committees (i) The women are in majority, (ii)The men are in majority
A committee of 12 is to be formed from 9 women and 8 men. In how many ways this can be if at least five women have to be in the committee? In how many ways in these committees (i) The women are in majority, (ii)The men are in majority
|
IIT 1994 |
05:51 min
|
|
453 |
The area enclosed between y = ax2 and x = ay2 (a > 0) is one square unit. Then the value of a is a) 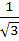 b)  c) 1 d) 
The area enclosed between y = ax2 and x = ay2 (a > 0) is one square unit. Then the value of a is a) 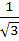 b)  c) 1 d) 
|
IIT 2004 |
04:13 min
|
|
454 |
Let f (x + y) = f (x) f (y) for all x, y. Suppose that f (5) = 2 and 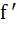 (0) = 3. Find f (0) = 3. Find f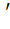 (5). (5). a) 1 b) 2 c) 3 d) 6
Let f (x + y) = f (x) f (y) for all x, y. Suppose that f (5) = 2 and 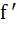 (0) = 3. Find f (0) = 3. Find f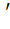 (5). (5). a) 1 b) 2 c) 3 d) 6
|
IIT 1981 |
03:33 min
|
|
455 |
If a function f : 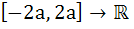 is an odd function such that is an odd function such that 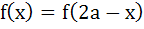 for x ε [a, 2a] and the left hand derivative at for x ε [a, 2a] and the left hand derivative at x = a is 0 then find the left hand derivative at x = 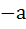 a) 0 b) 1 c) a d) 2a
If a function f : 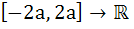 is an odd function such that is an odd function such that 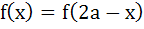 for x ε [a, 2a] and the left hand derivative at for x ε [a, 2a] and the left hand derivative at x = a is 0 then find the left hand derivative at x = 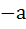 a) 0 b) 1 c) a d) 2a
|
IIT 2003 |
03:55 min
|
|
456 |
A country produces 90% of its food diet. The population grows continuously at a rate of 3% per year. Its annual food production every year is 4% more than that of last year. Assuming that the average food requirement per person remains constant, prove that the country will become self sufficient in food after n years, where n is the smallest integer bigger than or equal to 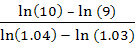
A country produces 90% of its food diet. The population grows continuously at a rate of 3% per year. Its annual food production every year is 4% more than that of last year. Assuming that the average food requirement per person remains constant, prove that the country will become self sufficient in food after n years, where n is the smallest integer bigger than or equal to 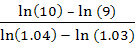
|
IIT 2000 |
04:17 min
|
|
457 |
If f(x) is a polynomial of degree less than or equal to 2 and S be the set of all such polynomials so that P(0) = 0 P(1) = 1, and 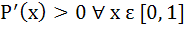
Then a) S = ɸ b) S = ax + (1 – a) x2 ⩝ a ε (0, 2) c) S = ax + (1 – a) x2 ⩝ a ε (0, ∞) d) S = ax + (1 – a) x2 ⩝ a ε (0, 1)
If f(x) is a polynomial of degree less than or equal to 2 and S be the set of all such polynomials so that P(0) = 0 P(1) = 1, and 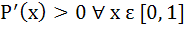
Then a) S = ɸ b) S = ax + (1 – a) x2 ⩝ a ε (0, 2) c) S = ax + (1 – a) x2 ⩝ a ε (0, ∞) d) S = ax + (1 – a) x2 ⩝ a ε (0, 1)
|
IIT 2005 |
02:32 min
|
|
458 |
The line 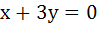 is a diameter of the circle is a diameter of the circle 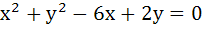 a) True b) False
The line 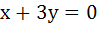 is a diameter of the circle is a diameter of the circle 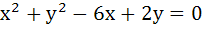 a) True b) False
|
IIT 1989 |
01:39 min
|
|
459 |
One or more correct answers
In a triangle PQR, sin P, sin Q, sin R are in arithmetic progression then a) Altitudes are in arithmetic progression b) Altitudes are in harmonic progression c) Medians are in geometric progression d) Medians are in arithmetic progression
One or more correct answers
In a triangle PQR, sin P, sin Q, sin R are in arithmetic progression then a) Altitudes are in arithmetic progression b) Altitudes are in harmonic progression c) Medians are in geometric progression d) Medians are in arithmetic progression
|
IIT 1998 |
03:36 min
|
|
460 |
f(x) is a function such that 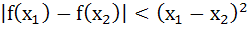 and the tangent at any point passes through (1, 2). Find the equation of the tangent. and the tangent at any point passes through (1, 2). Find the equation of the tangent. a) x = 2 b) y = 2 c) x + y = 2 d) x – y = 2
f(x) is a function such that 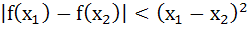 and the tangent at any point passes through (1, 2). Find the equation of the tangent. and the tangent at any point passes through (1, 2). Find the equation of the tangent. a) x = 2 b) y = 2 c) x + y = 2 d) x – y = 2
|
IIT 2005 |
03:06 min
|
|
461 |
The lines 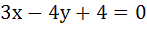 and and 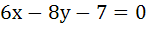 are tangents to the same circle. The radius of this circle is . . . . . are tangents to the same circle. The radius of this circle is . . . . .
The lines 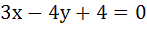 and and 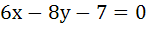 are tangents to the same circle. The radius of this circle is . . . . . are tangents to the same circle. The radius of this circle is . . . . .
|
IIT 1984 |
02:30 min
|
|
462 |
The external radii 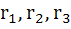 of ΔABC are in harmonic progression then prove that a, b, c are in arithmetic progression of ΔABC are in harmonic progression then prove that a, b, c are in arithmetic progression a) True b) False
The external radii 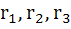 of ΔABC are in harmonic progression then prove that a, b, c are in arithmetic progression of ΔABC are in harmonic progression then prove that a, b, c are in arithmetic progression a) True b) False
|
IIT 1983 |
01:51 min
|
|
463 |
True / False If f (x) = ( a – xn )1/n where a > 0 and n is a positive integer then f ( f ( x ) ) = x. a) True b) False
True / False If f (x) = ( a – xn )1/n where a > 0 and n is a positive integer then f ( f ( x ) ) = x. a) True b) False
|
IIT 1983 |
01:23 min
|
|
464 |
Let f(x) = 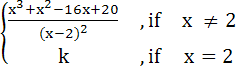 If f is continuous for all x, then k is equal to a) 3 b) 5 c) 7 d) 9
Let f(x) = 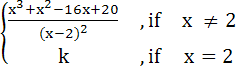 If f is continuous for all x, then k is equal to a) 3 b) 5 c) 7 d) 9
|
IIT 1981 |
03:32 min
|
|
465 |
Fill in the blank The domain of the function f (x) = 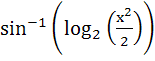 is is a) [− 2, − 1] b) [1, 2] c) [− 2, − 1] ⋃ [1, 2] d) None of the above
Fill in the blank The domain of the function f (x) = 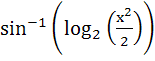 is is a) [− 2, − 1] b) [1, 2] c) [− 2, − 1] ⋃ [1, 2] d) None of the above
|
IIT 1984 |
02:48 min
|
|
466 |
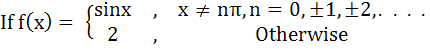
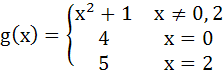
Then 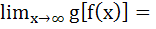
a) 0 b) 1 c) 2 d) 4
|
IIT 1981 |
01:26 min
|
|
467 |
The complex numbers 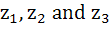 satisfying satisfying 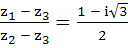 are the vertices of the triangle which is are the vertices of the triangle which is a) of zero area b) right angle isosceles c) equilateral d) obtuse angled isosceles
The complex numbers 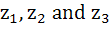 satisfying satisfying 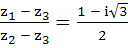 are the vertices of the triangle which is are the vertices of the triangle which is a) of zero area b) right angle isosceles c) equilateral d) obtuse angled isosceles
|
IIT 2001 |
05:10 min
|
|
468 |
Let x and y be two real variables such that x > 0 and xy = 1. Find the minimum value of x + y. a) 1 b) 2 c) 3 d) 4
Let x and y be two real variables such that x > 0 and xy = 1. Find the minimum value of x + y. a) 1 b) 2 c) 3 d) 4
|
IIT 1981 |
01:44 min
|
|
469 |
ABC is an isosceles triangle in a circle of radius r. If AB = AC and h is the altitude from A to BC then the triangle ABC has perimeter 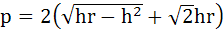 , area A = . . . . . , area A = . . . . . Also 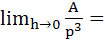 . . . . . . . . . .
ABC is an isosceles triangle in a circle of radius r. If AB = AC and h is the altitude from A to BC then the triangle ABC has perimeter 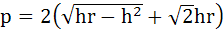 , area A = . . . . . , area A = . . . . . Also 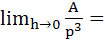 . . . . . . . . . .
|
IIT 1989 |
07:12 min
|
|
470 |
Let f(x) = x|x|. The set of points where f(x) is twice differentiable is . . . . a) ℝ b) 0 c) ℝ − {0, 1}
Let f(x) = x|x|. The set of points where f(x) is twice differentiable is . . . . a) ℝ b) 0 c) ℝ − {0, 1}
|
IIT 1992 |
02:00 min
|
|
471 |
Find the shortest distance of the point (0, c) from the parabola
y = x2, where 0 ≤ c ≤ 5. a) 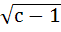 b) 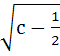 c) 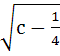 d) 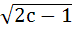
Find the shortest distance of the point (0, c) from the parabola
y = x2, where 0 ≤ c ≤ 5. a) 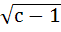 b) 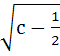 c) 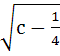 d) 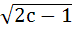
|
IIT 1982 |
03:58 min
|
|
472 |
Both roots of the equation ( x – b) ( x – c) + (x – c) ( x – a) + (x – a) (x – b) = 0 are always a) positive b) negative c) real d) none of these
Both roots of the equation ( x – b) ( x – c) + (x – c) ( x – a) + (x – a) (x – b) = 0 are always a) positive b) negative c) real d) none of these
|
IIT 1980 |
02:52 min
|
|
473 |
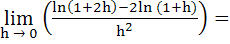
a) – 1 b) 0 c) 1 d) 2
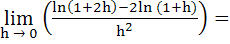
a) – 1 b) 0 c) 1 d) 2
|
IIT 1997 |
02:51 min
|
|
474 |
If 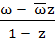 is purely real where ω = α + iβ, β ≠ 0 and z ≠ 1 then the set of real values of z is is purely real where ω = α + iβ, β ≠ 0 and z ≠ 1 then the set of real values of z is a) 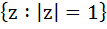 b) 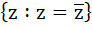 c) 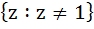 d) 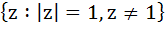
If 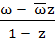 is purely real where ω = α + iβ, β ≠ 0 and z ≠ 1 then the set of real values of z is is purely real where ω = α + iβ, β ≠ 0 and z ≠ 1 then the set of real values of z is a) 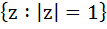 b) 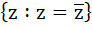 c) 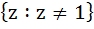 d) 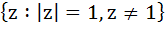
|
IIT 2006 |
05:43 min
|
|
475 |
Two vertices of an equilateral triangle are (- 1, 0) and (1, 0) and its third vertex lies above the X–axis, the equation of circumcircle is . . .
Two vertices of an equilateral triangle are (- 1, 0) and (1, 0) and its third vertex lies above the X–axis, the equation of circumcircle is . . .
|
IIT 1997 |
04:55 min
|