|
426 |
Fill in the blank The solution of the equation
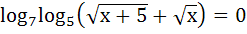 is ………….. is …………..
Fill in the blank The solution of the equation
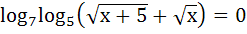 is ………….. is …………..
|
IIT 1986 |
02:04 min
|
|
427 |
If 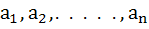 are in Arithmetic Progression where are in Arithmetic Progression where 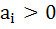 for all i, show that for all i, show that
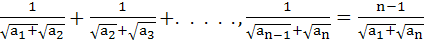
|
IIT 1982 |
04:29 min
|
|
428 |
Show that
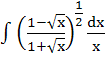 = = 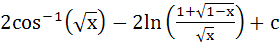
Show that
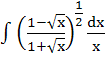 = = 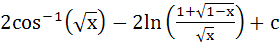
|
IIT 1997 |
04:06 min
|
|
429 |
Let a, b, c be three non co–planar vectors and p, q, r are vectors defined by the relations
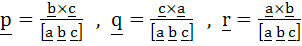
Then the value of the expression
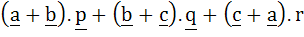 is equal to is equal to a) 0 b) 1 c) 2 d) 3
Let a, b, c be three non co–planar vectors and p, q, r are vectors defined by the relations
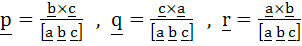
Then the value of the expression
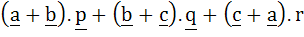 is equal to is equal to a) 0 b) 1 c) 2 d) 3
|
IIT 1988 |
05:35 min
|
|
430 |
Fill in the blank If x < 0, y < 0, 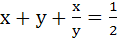 and and 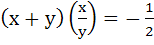 then x then x 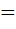 ……….. and y ……….. and y 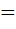 ……….. ………..
|
IIT 1990 |
04:06 min
|
|
431 |
The sum of the squares of three distinct real numbers which are in Geometric Progression is 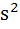 . If their sum is . If their sum is 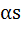 , show that , show that
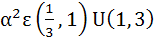
|
IIT 1986 |
06:02 min
|
|
432 |
Show that 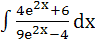 = = 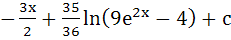
Show that 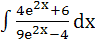 = = 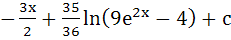
|
IIT 1990 |
07:54 min
|
|
433 |
Let 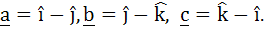 If d is a unit vector such that If d is a unit vector such that 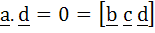 then d equals then d equals a) 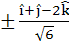 b) 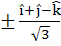 c) 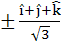 d) 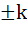
Let 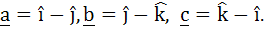 If d is a unit vector such that If d is a unit vector such that 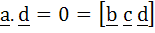 then d equals then d equals a) 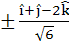 b) 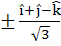 c) 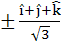 d) 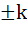
|
IIT 1995 |
04:16 min
|
|
434 |
(One or more correct answers)
Let E and F are two independent events. The probability that both E and F happen is 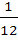 and the probability that neither E nor F happens is and the probability that neither E nor F happens is  , then , then a) 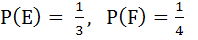 b) 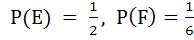 c) 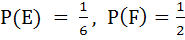 d) 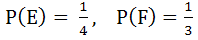
(One or more correct answers)
Let E and F are two independent events. The probability that both E and F happen is 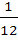 and the probability that neither E nor F happens is and the probability that neither E nor F happens is  , then , then a) 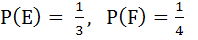 b) 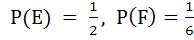 c) 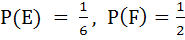 d) 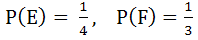
|
IIT 1993 |
04:01 min
|
|
435 |
If 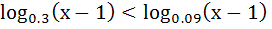 then x lies in the interval then x lies in the interval a) (2, ∞) b) (1, 2) c) (−2, −1) d) None of these
If 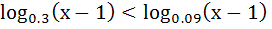 then x lies in the interval then x lies in the interval a) (2, ∞) b) (1, 2) c) (−2, −1) d) None of these
|
IIT 1985 |
03:00 min
|
|
436 |
The value of the integral
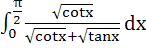 is is a) 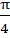 b)  c) π d) None of these
The value of the integral
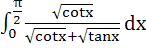 is is a) 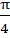 b)  c) π d) None of these
|
IIT 1983 |
02:20 min
|
|
437 |
Six boys and six girls sit in a row at random. Find the probability that the six girls sit together,
Six boys and six girls sit in a row at random. Find the probability that the six girls sit together,
|
IIT 1999 |
04:10 min
|
|
438 |
Given A = 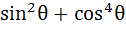 for all values of θ, then for all values of θ, then a) 1 ≤ A ≤ 2 b)  ≤ A ≤ 1 ≤ A ≤ 1 c) 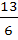 ≤ A ≤ 1 ≤ A ≤ 1 d)  ≤ A ≤ ≤ A ≤ 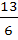
Given A = 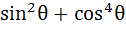 for all values of θ, then for all values of θ, then a) 1 ≤ A ≤ 2 b)  ≤ A ≤ 1 ≤ A ≤ 1 c) 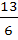 ≤ A ≤ 1 ≤ A ≤ 1 d)  ≤ A ≤ ≤ A ≤ 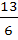
|
IIT 1980 |
01:38 min
|
|
439 |
If a, b, c are in Arithmetic Progression and 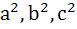 are in Harmonic Progression then prove that either are in Harmonic Progression then prove that either 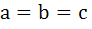 or a, b and or a, b and 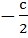 are in Geometric Progression. are in Geometric Progression.
|
IIT 2003 |
03:47 min
|
|
440 |
The value of 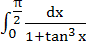 is is a) 0 b) 1 c)  d) 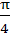
The value of 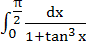 is is a) 0 b) 1 c)  d) 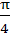
|
IIT 1993 |
02:12 min
|
|
441 |
A and B are two candidates seeking admission in IIT. The probability that A is selected is 0.5 and the probability of A and B being selected is at most 0.3. Is it possible that the probability of B being selected is 0.9?
A and B are two candidates seeking admission in IIT. The probability that A is selected is 0.5 and the probability of A and B being selected is at most 0.3. Is it possible that the probability of B being selected is 0.9?
|
IIT 1982 |
01:34 min
|
|
442 |
If y is a function of x and ln (x + y) – 2xy = 0 then the value of y’ (0) is equal to a) 1 b) – 1 c) 2 d) 0
If y is a function of x and ln (x + y) – 2xy = 0 then the value of y’ (0) is equal to a) 1 b) – 1 c) 2 d) 0
|
IIT 2004 |
01:56 min
|
|
443 |
If 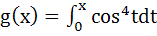 then g(x + π) equals then g(x + π) equals a) g(x) + g(π) b) g(x) − g(π) c) g(x) g(π) d) 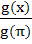
If 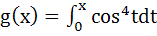 then g(x + π) equals then g(x + π) equals a) g(x) + g(π) b) g(x) − g(π) c) g(x) g(π) d) 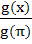
|
IIT 1997 |
05:05 min
|
|
444 |
If 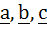 are unit vectors, then are unit vectors, then 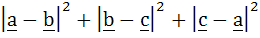 does not exceed does not exceed a) 4 b) 9 c) 8 d) 6
If 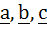 are unit vectors, then are unit vectors, then 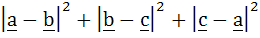 does not exceed does not exceed a) 4 b) 9 c) 8 d) 6
|
IIT 2001 |
04:28 min
|
|
445 |
In a city only two news papers A and B are published. It is known that 25% of the city population read A and 20% read B, while 8% read A and B. It is also known that 30% of those who read A but not B and 40% of those who read B but not A look into the advertisement. 50% of those who read both A and B look into the advertisement. What is the percentage of the population that reads an advertisement?
In a city only two news papers A and B are published. It is known that 25% of the city population read A and 20% read B, while 8% read A and B. It is also known that 30% of those who read A but not B and 40% of those who read B but not A look into the advertisement. 50% of those who read both A and B look into the advertisement. What is the percentage of the population that reads an advertisement?
|
IIT 1984 |
02:57 min
|
|
446 |
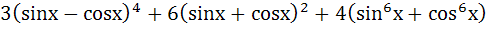
a) 11 b) 12 c) 13 d) 14
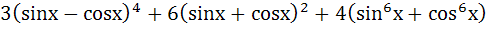
a) 11 b) 12 c) 13 d) 14
|
IIT 1995 |
04:20 min
|
|
447 |
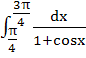 is equal to is equal to
a) 2 b) –2 c)  d) 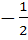
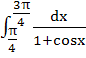 is equal to is equal to
a) 2 b) –2 c)  d) 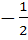
|
IIT 1999 |
03:25 min
|
|
448 |
Let 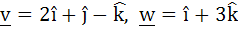 and u is a unit vector then the maximum value of and u is a unit vector then the maximum value of 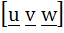 is is a) 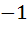 b) 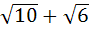 c) 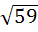 d) 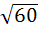
Let 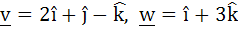 and u is a unit vector then the maximum value of and u is a unit vector then the maximum value of 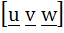 is is a) 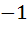 b) 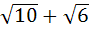 c) 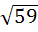 d) 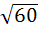
|
IIT 2003 |
02:32 min
|
|
449 |
Given both θ and Ф are acute angles and sinθ =  , cos Ф = , cos Ф =  then the value of θ + Ф belongs to then the value of θ + Ф belongs to a) 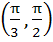 b) 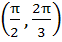 c) 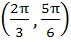 d) 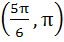
Given both θ and Ф are acute angles and sinθ =  , cos Ф = , cos Ф =  then the value of θ + Ф belongs to then the value of θ + Ф belongs to a) 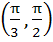 b) 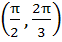 c) 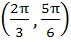 d) 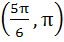
|
IIT 2004 |
02:15 min
|
|
450 |
Let x be the Arithmetic Mean and y, z be two Geometric Means between any two positive numbers then 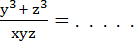
Let x be the Arithmetic Mean and y, z be two Geometric Means between any two positive numbers then 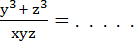
|
IIT 1997 |
02:27 min
|