|
401 |
Let A be a set containing n elements. A subset P of A is constructed at random. The set A is reconstructed by replacing the elements of P. A subset of Q of A is again chosen at random. Find the probability that P and Q have no elements in common.
Let A be a set containing n elements. A subset P of A is constructed at random. The set A is reconstructed by replacing the elements of P. A subset of Q of A is again chosen at random. Find the probability that P and Q have no elements in common.
|
IIT 1990 |
04:10 min
|
|
402 |
The derivative of an even function is always an odd function. a) False b) True
The derivative of an even function is always an odd function. a) False b) True
|
IIT 1983 |
01:33 min
|
|
403 |
If 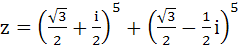 then then a) Re(z) = 0 b) Im(z) = 0 c) Re(z) = 0, Im(z) > 0 d) Re(z) > 0, Im(z) < 0
If 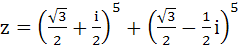 then then a) Re(z) = 0 b) Im(z) = 0 c) Re(z) = 0, Im(z) > 0 d) Re(z) > 0, Im(z) < 0
|
IIT 1982 |
02:07 min
|
|
404 |
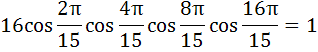
a) True b) False
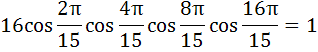
a) True b) False
|
IIT 1983 |
03:16 min
|
|
405 |
The derivative of 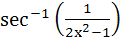 with respect to with respect to 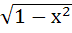 at x = at x =  is is a) 0 b) 1 c) 2 d) 4
The derivative of 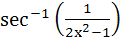 with respect to with respect to 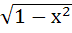 at x = at x =  is is a) 0 b) 1 c) 2 d) 4
|
IIT 1986 |
04:19 min
|
|
406 |
If f (x) is differentiable and 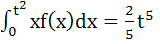 , then , then 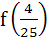 equals equals a)  b) 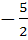 c) 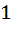 d) 
If f (x) is differentiable and 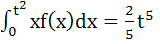 , then , then 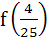 equals equals a)  b) 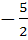 c) 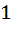 d) 
|
IIT 2004 |
01:33 min
|
|
407 |
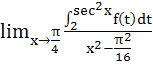 equals equals
a) 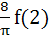 b) 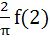 c) 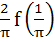 d) 4 f (2)
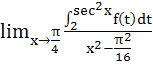 equals equals
a) 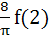 b) 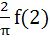 c) 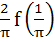 d) 4 f (2)
|
IIT 2007 |
03:41 min
|
|
408 |
Let z and ω be two non zero complex numbers such that |z| = |ω| and Arg(z) + Arg(ω) = π then z equals a) ω b) 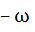 c) 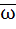 d) 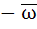
Let z and ω be two non zero complex numbers such that |z| = |ω| and Arg(z) + Arg(ω) = π then z equals a) ω b) 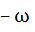 c) 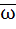 d) 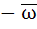
|
IIT 1995 |
02:03 min
|
|
409 |
The function 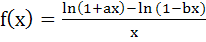 is not defined at x = 0. The value which should be assigned to f at x = 0 so that it is continuous at x = 0 is is not defined at x = 0. The value which should be assigned to f at x = 0 so that it is continuous at x = 0 is a) a – b b) a + b c) lna – lnb d) None of these
The function 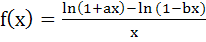 is not defined at x = 0. The value which should be assigned to f at x = 0 so that it is continuous at x = 0 is is not defined at x = 0. The value which should be assigned to f at x = 0 so that it is continuous at x = 0 is a) a – b b) a + b c) lna – lnb d) None of these
|
IIT 1983 |
02:48 min
|
|
410 |
Find the value of 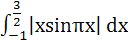 a) 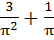 b) 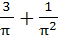 c) 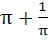 d) 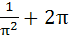
Find the value of 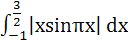 a) 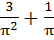 b) 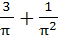 c) 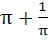 d) 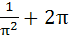
|
IIT 1982 |
07:35 min
|
|
411 |
The set of lines 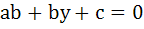 where where 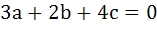 is concurrent at the point . . . is concurrent at the point . . .
The set of lines 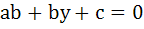 where where 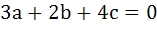 is concurrent at the point . . . is concurrent at the point . . .
|
IIT 1982 |
01:51 min
|
|
412 |
If tan θ = 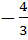 then sin θ is then sin θ is a) 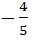 but not but not  b) 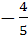 or or  c)  but not − but not −  d) None of these
If tan θ = 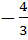 then sin θ is then sin θ is a) 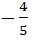 but not but not  b) 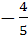 or or  c)  but not − but not −  d) None of these
|
IIT 1978 |
02:26 min
|
|
413 |
Find the sum of the series
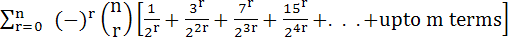
Find the sum of the series
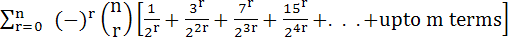
|
IIT 1985 |
03:46 min
|
|
414 |
The set of all points where the function 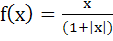 is differentiable is is differentiable is a) 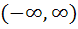 b) [0, ∞) c) 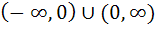 d) (0, ∞) e) None of these
The set of all points where the function 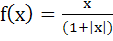 is differentiable is is differentiable is a) 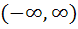 b) [0, ∞) c) 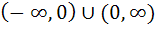 d) (0, ∞) e) None of these
|
IIT 1987 |
04:36 min
|
|
415 |
Given a function f (x) such that
i) it is integrable over every interval on the real axis and
ii) f (t + x) = f (x) for every x and a real t, then show that the integral 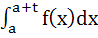 is independent of a. is independent of a.
Given a function f (x) such that
i) it is integrable over every interval on the real axis and
ii) f (t + x) = f (x) for every x and a real t, then show that the integral 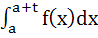 is independent of a. is independent of a.
|
IIT 1984 |
02:15 min
|
|
416 |
If the algebraic sum of the perpendicular distance from the point
(2, 0), (0, 2) and (1, 1) to a variable straight line be zero then the line passes through a fixed point whose coordinates are
If the algebraic sum of the perpendicular distance from the point
(2, 0), (0, 2) and (1, 1) to a variable straight line be zero then the line passes through a fixed point whose coordinates are
|
IIT 1991 |
03:15 min
|
|
417 |
The general solution of
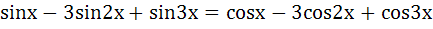 is is a) 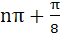 b) 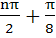 c) 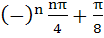 d) 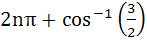
The general solution of
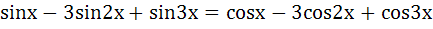 is is a) 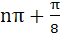 b) 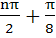 c) 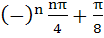 d) 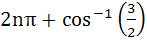
|
IIT 1989 |
03:28 min
|
|
418 |
The function f(x) = 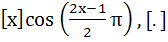 denotes the greatest integer function is discontinuous at denotes the greatest integer function is discontinuous at a) All x b) All integer points c) No x d) x which is not an integer
The function f(x) = 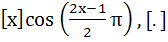 denotes the greatest integer function is discontinuous at denotes the greatest integer function is discontinuous at a) All x b) All integer points c) No x d) x which is not an integer
|
IIT 1993 |
03:16 min
|
|
419 |
If f (x) and g (x) are continuous functions on (0, a) satisfying f (x) = f (a – x) and g (x) + g (a – x) = 2 then show that 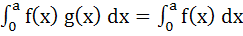
If f (x) and g (x) are continuous functions on (0, a) satisfying f (x) = f (a – x) and g (x) + g (a – x) = 2 then show that 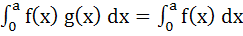
|
IIT 1989 |
02:36 min
|
|
420 |
The equation of the circles through (1, 1) and the point of intersection of
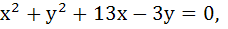
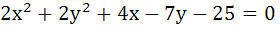 is is a) 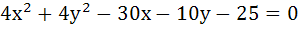 b) 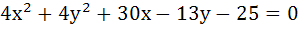 c) 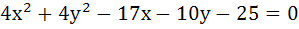 d) None of these
The equation of the circles through (1, 1) and the point of intersection of
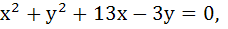
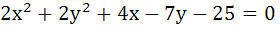 is is a) 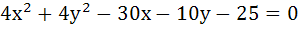 b) 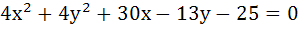 c) 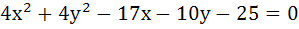 d) None of these
|
IIT 1983 |
02:31 min
|
|
421 |
The general value of θ satisfying the equation
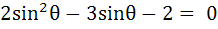 is is a) 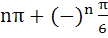 b) 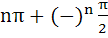 c) 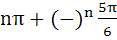 d) 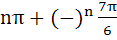
The general value of θ satisfying the equation
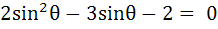 is is a) 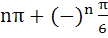 b) 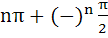 c) 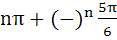 d) 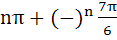
|
IIT 1995 |
01:18 min
|
|
422 |
A cubic f (x) vanishes at x = −2 and has a relative minimum/maximum at x = −1 and 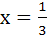 . If . If 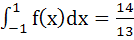 , find the cube f (x). , find the cube f (x). a) x3 + x2 + x + 1 b) x3 + x2 − x + 1 c) x3 − x2 + x + 2 d) x3 + x2 − x + 2
A cubic f (x) vanishes at x = −2 and has a relative minimum/maximum at x = −1 and 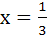 . If . If 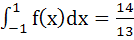 , find the cube f (x). , find the cube f (x). a) x3 + x2 + x + 1 b) x3 + x2 − x + 1 c) x3 − x2 + x + 2 d) x3 + x2 − x + 2
|
IIT 1992 |
05:24 min
|
|
423 |
If a circle passes through the points (a, b) and cuts the circle 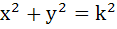 orthogonally, then the equation of the locus of its centre is orthogonally, then the equation of the locus of its centre is a) 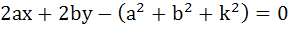 b) 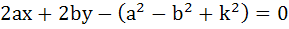 c) 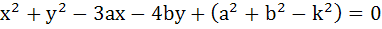 d) 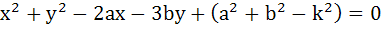
If a circle passes through the points (a, b) and cuts the circle 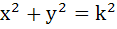 orthogonally, then the equation of the locus of its centre is orthogonally, then the equation of the locus of its centre is a) 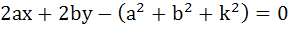 b) 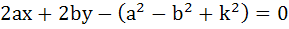 c) 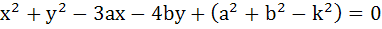 d) 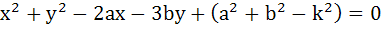
|
IIT 1988 |
04:03 min
|
|
424 |
In ΔPQR, angle R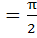 . If tan . If tan  and tan and tan  are roots of the equation are roots of the equation 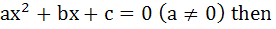 a) 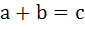 b) 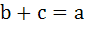 c) 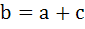 d) 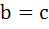
|
IIT 1999 |
02:23 min
|
|
425 |
Prove that 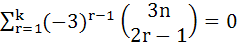
where 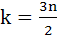 and n is an even integer. and n is an even integer.
Prove that 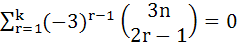
where 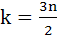 and n is an even integer. and n is an even integer.
|
IIT 1993 |
09:38 min
|