|
251 |
Let In represents area of n sided regular polygon inscribed in a unit circle and On the area of n–sided regular polygon circumscribing it. Prove that 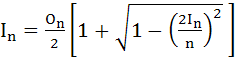
Let In represents area of n sided regular polygon inscribed in a unit circle and On the area of n–sided regular polygon circumscribing it. Prove that 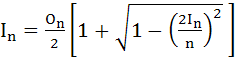
|
IIT 2003 |
07:43 min
|
|
252 |
P(x) is a polynomial function such that P(1) = 0, 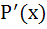 > P(x) > P(x)  x > 1. Then x > 1. Then 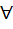 x > 1, x > 1,
a) P(x) > 0 b) P(x) = 0 c) P(x) < 1
P(x) is a polynomial function such that P(1) = 0, 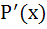 > P(x) > P(x)  x > 1. Then x > 1. Then  x > 1, x > 1,
a) P(x) > 0 b) P(x) = 0 c) P(x) < 1
|
IIT 2003 |
02:15 min
|
|
253 |
Prove that
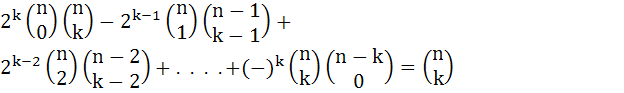
Prove that
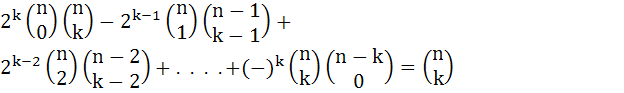
|
IIT 2003 |
05:28 min
|
|
254 |
Minimum area of the triangle formed by the tangent to the ellipse 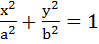 with co-ordinate axes is with co-ordinate axes is
a) 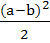 b) 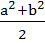 c) 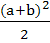 d) ab
Minimum area of the triangle formed by the tangent to the ellipse 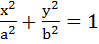 with co-ordinate axes is with co-ordinate axes is
a) 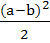 b) 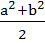 c) 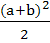 d) ab
|
IIT 2005 |
02:43 min
|
|
255 |
If A and B are points in the plane such that 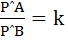 (constant) for all P on a given circle then the value of k cannot be equal to - - - - -. (constant) for all P on a given circle then the value of k cannot be equal to - - - - -.
If A and B are points in the plane such that 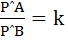 (constant) for all P on a given circle then the value of k cannot be equal to - - - - -. (constant) for all P on a given circle then the value of k cannot be equal to - - - - -.
|
IIT 1982 |
04:30 min
|
|
256 |
Let {x} and [x] denote the fractional and integral part of a real number respectively. Solve 4 {x} = x + [x] a) x = 0 b) 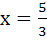 c) 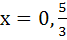 d) 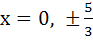
Let {x} and [x] denote the fractional and integral part of a real number respectively. Solve 4 {x} = x + [x] a) x = 0 b) 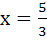 c) 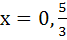 d) 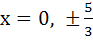
|
IIT 1994 |
03:11 min
|
|
257 |
The sides AB, BC and CA of a triangle ABC have 3, 4 and 5 interior points respectively on them. The number of triangles that can be constructed using these interior points as vertices is . . . .
The sides AB, BC and CA of a triangle ABC have 3, 4 and 5 interior points respectively on them. The number of triangles that can be constructed using these interior points as vertices is . . . .
|
IIT 1984 |
04:31 min
|
|
258 |
Multiple choice Let h(x) = f(x) – (f(x))2 + (f(x))3 for every real number x, then a) h increases whenever f is increasing b) h is increasing whenever f is decreasing c) h is decreasing whenever f is decreasing d) nothing can be said in general
Multiple choice Let h(x) = f(x) – (f(x))2 + (f(x))3 for every real number x, then a) h increases whenever f is increasing b) h is increasing whenever f is decreasing c) h is decreasing whenever f is decreasing d) nothing can be said in general
|
IIT 1998 |
02:37 min
|
|
259 |
From the origin chords are drawn to the circle 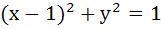 . The equation of the locus of the mid points of these chords is . . . . . . The equation of the locus of the mid points of these chords is . . . . .
From the origin chords are drawn to the circle 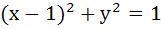 . The equation of the locus of the mid points of these chords is . . . . . . The equation of the locus of the mid points of these chords is . . . . .
|
IIT 1984 |
02:45 min
|
|
260 |
If 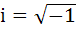 then then 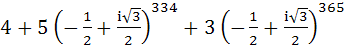 equals equals a) 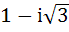 b) 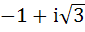 c) 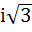 d) 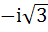
If 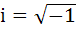 then then 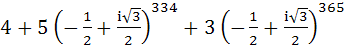 equals equals a) 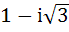 b) 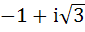 c) 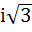 d) 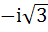
|
IIT 1999 |
03:27 min
|
|
261 |
The area of the triangle formed by the tangents from the point (4, 3) to the circle 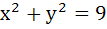 and the line joining their point of contact is . and the line joining their point of contact is .
The area of the triangle formed by the tangents from the point (4, 3) to the circle 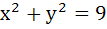 and the line joining their point of contact is . and the line joining their point of contact is .
|
IIT 1987 |
06:00 min
|
|
262 |
L = 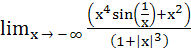 = . . . . = . . . . a) – 1 b) 0 c) 1 d) 2
L = 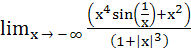 = . . . . = . . . . a) – 1 b) 0 c) 1 d) 2
|
IIT 1987 |
02:12 min
|
|
263 |
Let 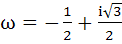 then the value of then the value of 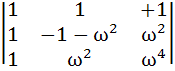 is is a) 3ω b) 3ω(ω – 1) c) 3ω2 d) 3ω(1 – ω)
Let 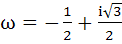 then the value of then the value of 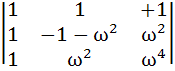 is is a) 3ω b) 3ω(ω – 1) c) 3ω2 d) 3ω(1 – ω)
|
IIT 2002 |
03:39 min
|
|
264 |
The area of triangle formed by the positive X–axis and the normal and tangent to the circle 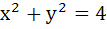 at at 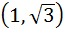 is . . . . . . is . . . . . .
The area of triangle formed by the positive X–axis and the normal and tangent to the circle 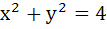 at at 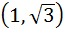 is . . . . . . is . . . . . .
|
IIT 1989 |
02:40 min
|
|
265 |
Intercepts on the line y = x by the circle 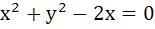 is AB. Equation of the circle with AB as diameter is . . . . . is AB. Equation of the circle with AB as diameter is . . . . .
Intercepts on the line y = x by the circle 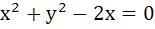 is AB. Equation of the circle with AB as diameter is . . . . . is AB. Equation of the circle with AB as diameter is . . . . .
|
IIT 1996 |
03:14 min
|
|
266 |
The number of real solutions of the equation | x |2 – 3 | x | + 2 = 0 is a) 4 b) 1 c) 3 d) 2
The number of real solutions of the equation | x |2 – 3 | x | + 2 = 0 is a) 4 b) 1 c) 3 d) 2
|
IIT 1982 |
01:27 min
|
|
267 |
Match the following Let the function defined in column 1 has domain 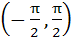 | Column 1 | Column 2 | | i) x + sinx | A)increasing | | ii) secx | B) decreasing | | | C)neither increasing nor decreasing | a) i) → A, ii) → B b) i) → A, ii) → C c) i) → C, ii) → A d) i) → B, ii) → C
Match the following Let the function defined in column 1 has domain 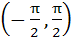 | Column 1 | Column 2 | | i) x + sinx | A)increasing | | ii) secx | B) decreasing | | | C)neither increasing nor decreasing | a) i) → A, ii) → B b) i) → A, ii) → C c) i) → C, ii) → A d) i) → B, ii) → C
|
IIT 1992 |
02:39 min
|
|
268 |
A man walks a distance of three units from the origin towards north-east (N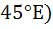 direction. From there he walks a distance of 4 units towards north–west (N direction. From there he walks a distance of 4 units towards north–west (N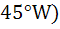 direction to reach a point P. Then the position of P in the argand plane is direction to reach a point P. Then the position of P in the argand plane is a) 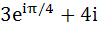 b) 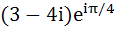 c) 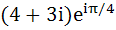 d) 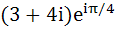
A man walks a distance of three units from the origin towards north-east (N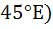 direction. From there he walks a distance of 4 units towards north–west (N direction. From there he walks a distance of 4 units towards north–west (N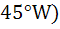 direction to reach a point P. Then the position of P in the argand plane is direction to reach a point P. Then the position of P in the argand plane is a) 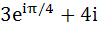 b) 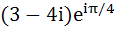 c) 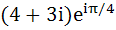 d) 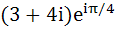
|
IIT 2007 |
05:31 min
|
|
269 |
Find the coordinates of the point on the curve 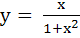 where the tangent to the curve has the greatest slope. where the tangent to the curve has the greatest slope. a) (0, 0) b) 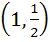 c) 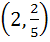 d) 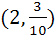
Find the coordinates of the point on the curve 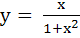 where the tangent to the curve has the greatest slope. where the tangent to the curve has the greatest slope. a) (0, 0) b) 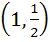 c) 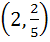 d) 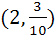
|
IIT 1984 |
06:59 min
|
|
270 |
If p, q, r are any real numbers, then a) Max ( p, q ) < max ( p, q, r ) b) Min ( p, q ) =  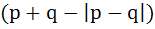 c) Max ( p, q ) < min ( p, q, r ) d) none of these
If p, q, r are any real numbers, then a) Max ( p, q ) < max ( p, q, r ) b) Min ( p, q ) =  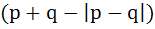 c) Max ( p, q ) < min ( p, q, r ) d) none of these
|
IIT 1982 |
01:52 min
|
|
271 |
Show that, if 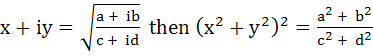
a, b, c, d ε ℝ
Show that, if 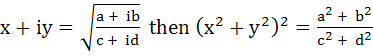
a, b, c, d ε ℝ
|
IIT 1978 |
02:04 min
|
|
272 |
The equation of the common tangent touching the circle
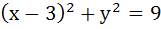 and the parabola and the parabola 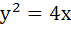 , above X–axis is , above X–axis is a) 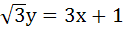 b) 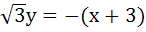 c) 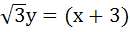 d) 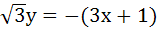
The equation of the common tangent touching the circle
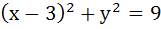 and the parabola and the parabola 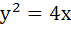 , above X–axis is , above X–axis is a) 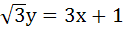 b) 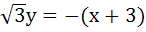 c) 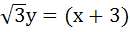 d) 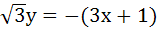
|
IIT 2001 |
05:54 min
|
|
273 |
The expression 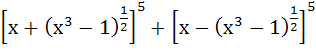 is a polynomial of degree is a polynomial of degree a) 5 b) 6 c) 7 d) 8
The expression 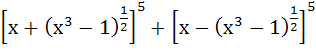 is a polynomial of degree is a polynomial of degree a) 5 b) 6 c) 7 d) 8
|
IIT 1992 |
03:38 min
|
|
274 |
If f(x) = 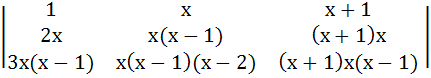
then f(100) equals a) 0 b) 1 c) 100 d) −100
If f(x) = 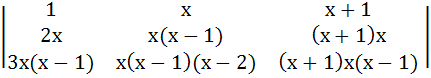
then f(100) equals a) 0 b) 1 c) 100 d) −100
|
IIT 1999 |
02:18 min
|
|
275 |
Show that the area of the triangle on the argand diagram formed by the complex numbers z, iz, z + iz is 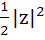 . .
Show that the area of the triangle on the argand diagram formed by the complex numbers z, iz, z + iz is 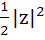 . .
|
IIT 1986 |
03:10 min
|